MATH 1140 Test
There are 30 points on this test. Show your work where possible.
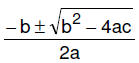
1. (1 pt) Solve exactly : (13x – 516)^2 = 7
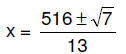
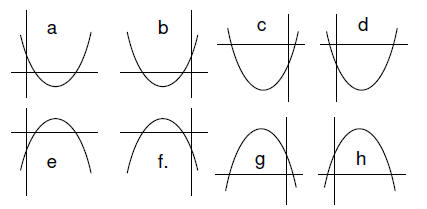
2. (2 pts) Give the correct graphs for
h: f(x) = -400x^2 + 5000x + 276
d: f(x) = 400x^2 – 5000x – 276
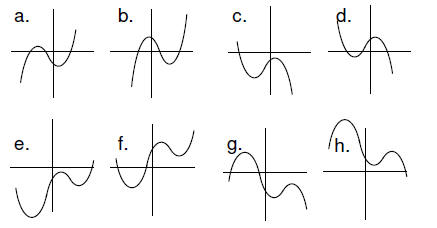
3. (3 pts) Choose the best graph for each polynomial
h: y(x) = -50x^4 + 70x^2 +10
c: y(x) = -50x^3 – 70x^2 –10
h: y(x) = -50x^4 – 70x^2 +10
4. (1 pt) Give the minimum degree of this polynomial : degree ≥ 6
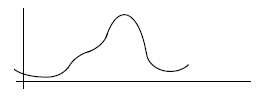
5. (3 pts) Give three different polynomials of degree 13,
each with zeroes at
x = 3, -5.7, π, and nowhere else.
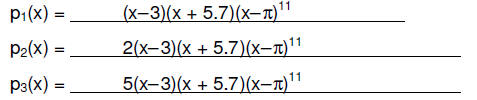
6. (3 pts) Choose the correct graph for each function
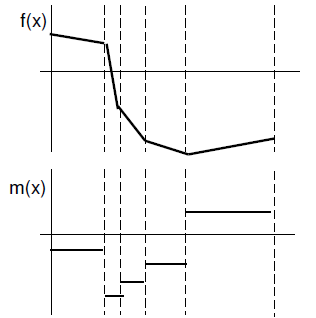
7. (2 pts) Sketch below f(x) the slope
function m(x). Indicate where m(x) is
positive , negative, zero, increasing or
decreasing.
8. (2 pts) Factor p (x) = 3x^2 + 3.6x – 31.59.
p(x) = 3(x – 2.7)(x + 3.9)
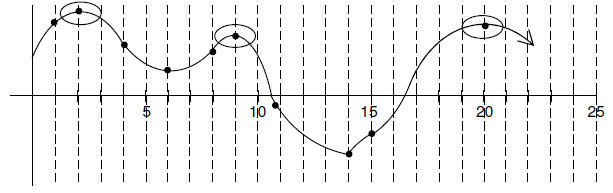
9. (1 pt) The function below has relative
maxima at: x = 2, 9, 20
10. (3 pts) Solve 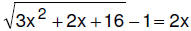 exactly.
exactly.
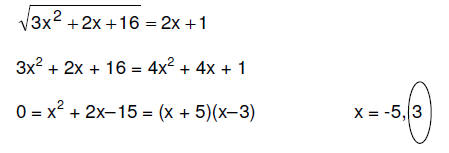
11. (4 pts) If producing x tons of a commodity yields a
profit (in dollars) of
P(x) = -.03x^2 + 805x – 2,000,000,
a. Find the production level that yields the maximum
profit.
-b/(2a) = 13416.7
b. Find the maximum profit.
P(-b/(2a) = 3400208.3
c. Find the break-even production levels .
P(x) = -.03x^2 + 805x – 2,000,000 = 0
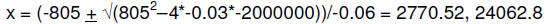
d. Find the production levels that keep profits above 3 million dollars.
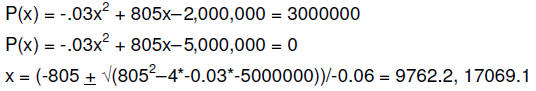
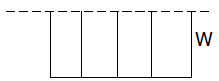
12. (2 pts) A rancher needs to enclose four
adjacent corrals as shown. A river forms one side
of the corrals, and 1350 yd of fencing is
available.
a. Give the area A = LW as a quadratic function of just
the variable W.
5W + L = 1350 A = (1350 – 5W)W
b. Give the width W that maximizes the area A(W)
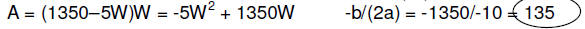
13. (3 pts) Factor p (x) = 2x^4 – 14.58x^2 – 4x – 10.8 given that p(-2.7) = 0.
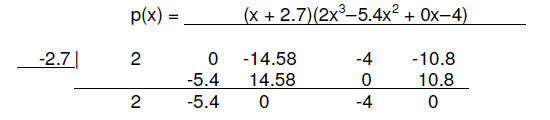
| Prev | Next |