Math ASSIGNMENT 9 SOLUTIONS

1. Let f . (a, b) -> R be continuous, with (a, b) 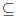R. Show that if f(r) = 0 for each rational
number r ∈(a, b), then f(x) = 0 for all x ∈(a, b).

Every real number x ∈(a, b) can be written as a limit of a sequence of rational numbers,
{r_n}. Thus, since f is continuous,

Thus, f(x) = 0 for all x ∈(a, b).

2. Let f . (a, b) -> R and g . (a, b) -> R be continuous, with (a, b) 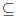R, so that f(r) = g(r) for
each rational number r ∈(a, b). Prove that f(x) = g(x) for all x ∈(a, b).

We will use the previous problem . We know that f(r) = g(r) for all rational numbers in
(a, b). Thus, define h(x) = f(x)-g(x). Then, h is continuous and h(r) = 0 for every rational
number in (a, b). Thus, h(x) = 0 for all x ∈(a, b). Therefore, f(x)-g(x) = 0 for all x ∈(a, b)
and the conclusion follows.

3. Define the function f by

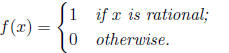
Show that f is discontinuous at every x ∈R.

We will show that it is discontinuous at each rational and at each irrational. Note that each
rational number can be written as the limit of a sequence of rational numbers,
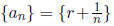
for n sufficiently large. Likewise , it can be written as the limit of a sequence of irrational
numbers, 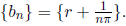Thus, if f is continuous at r we would have to have that

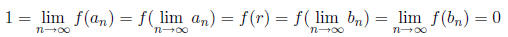
which cannot be, so f cannot be continuous at any rational number .
The similar argument will work to show that f is not continuous at any irrational number.

4. Define the function h by

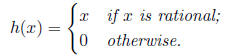
Show that h is continuous at x = 0 and at no other point.

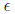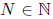Let {x_n} be any sequence that converges to 0. Then given any > 0 there is an so
that if n > N then 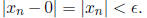. When we apply h to this sequence, we get a sequence
that is x_n if x_n is irrational and 0 if x_n is rational. However, since {x_n} converges to 0, we
can show that for any 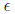> 0 we can find an N ∈N so that if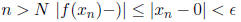
so the sequence 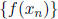converges and f is continuous at x = 0.

If x ≠ 0, then let 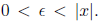If x ∈Q then h(x) = 0, but there exists a sequence of
irrational numbers converging to x and the sequence 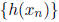will also converge to x but
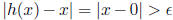so that h cannot be continuous at x. If x ∈R\Q, there is a sequence
of rationals that converges to x but whose functional values are all 0. Again, the function
does not take a sequence convergent to x to a sequence convergent to h(x), so it cannot be
continuous at any x ∈R\Q.

5. For each rational number x, write x as p/q where p and q are integers with no common factors
and q > 0. Define the function g by

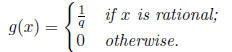
Thus, g(x) = 1 for all integers, 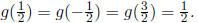Show that g is continuous at each
irrational and discontinuous at each rational.

First, note that for any x ∈R there is an n ∈Z and a ∈(0, 1) so that x = n + a and
g(x) = g(n + a). If x is irrational, then so is a and we have that g(x) = g(a) = 0. If x is
rational, then so is a and g(x) = g(a). Thus, to understand g it suffices to look at the values
of g for x ∈(0, 1).

Any irrational number, a, has a non-repeating decimal and we can consider that decimal
expansion as one sequence converging to a. Given any > 0 there is an so that
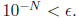Thus, the sequence 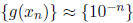converges to 0.

Now we need to show this for any sequence {x_n} converging to a. Let 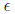> 0 and a ∈(0, 1)\Q.
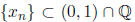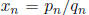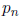Let so that x_n -> a. We can write with and 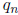relatively
prime. We need to show that 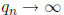as n goes to infinity. If that is true, then
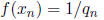
will go to 0 = f(a).

To show that 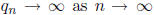, we will assume not. Thus, there is an M ∈N so that
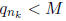for k = 1, 2, 3, . . . . This means then that there are only a finite number of fractions
of the form 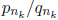in (0, 1) with 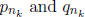relatively prime. This means then that the set
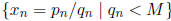is finite. Thus, the limit of this sequence is a member of the sequence,
i.e., a = p/q so that q < M. Thus, a ∈Q. This is a contradiction. Thus, the denominators
of the fractions must go to infinity and for any sequence {x_n} converging to an irrational a,
the sequence 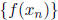converges to 0 = f(a) and the function is continuous at a.

If r ∈Q and r = p/q , then g(r) = 1/q. Choose 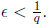Now, for any sequence converging to r
that contains irrational numbers 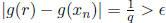so there is no way to guarantee that
for all n sufficiently large the values of g are close to g(r). Thus, g is not continuous at r.

6. Let f and g be continuous functions on [a, b] such that f(a) ≥ g(a) and f(b) ≤ g(b). Prove
that

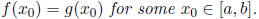
Define a function h(x) = g(x) - f(x) on [a, b]. Then note that h is continuous and h(a) =
g(a) - f(a) ≤ 0 and h(b) = g(b) - f(b) ≥ 0. If h(a) = 0, then f(a) = g(a) and we are done.
Likewise , if h(b) = 0 then f(b) = g(b) and we are done. Thus, assume that h(a) ≠ 0 (so
h(a) < 0) and assume that h(b) ≠ 0 (so h(b) > 0). Therefore, by the Intermediate Value
Theorem, there is an x₀ ∈(a, b) so that h(x₀) = 0 and this implies that f(x₀) = g(x₀).

7. Prove that 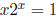for some x ∈(0, 1).

Define a function f on the interval [0, 1] by f(x) = 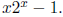Then note that f is continuous
and f(0) = -1 < 0 and f(1) = 1 > 0. Therefore, by the Intermediate Value Theorem , there
is an x ∈(0, 1) so that f(x) = 0. At that point we have

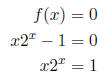
for some x ∈(0, 1).