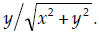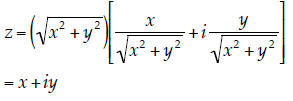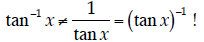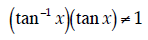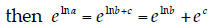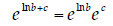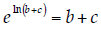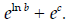MATH CONCEPTS: EXAM II
Skill Testing. (36 points, 3 pts each) The following problems are
meant to evaluate your ability to use
mathematical concepts . Unless you’re asked to, there is no need to explain what
you’re doing in this section; I’ll
mostly be looking for correct answers. In other words, don’t spend a lot of time
on these! However, you do want
to show some work for partial credit… don’t just write down the answers! YOU
CAN USE THE
ANSWERS FROM PREVIOUS PROBLEMS WITHOUT RE-WORKING THEM! (Just refer back to
them.)
1. Determinants. Find the determinant |B| of the following matrix:
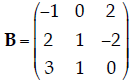
| Using the definition of the determinant for a 3×3 matrix, we have:
|
2. Cramer’ s Rule . Use Cramer’s rule to find the value of z that will
satisfy the following set of
inhomogeneous linear equations : (note that you only need to solve for z!)
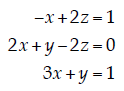
| In matrix notation, the above equations can be written as
Using Cramer’s rule, the value of z is given by:
Note that the value for the denominator was found in question 1. |
3. Transpose. Find the transpose (AT) of the following matrix:
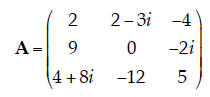
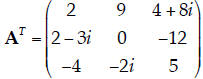 |
4. Adjoint. Find the adjoint (A+) of the matrix A given in question 3.
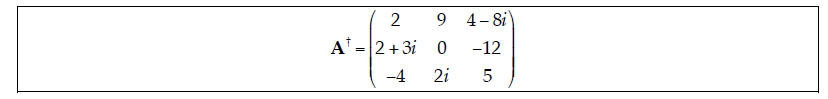
5. Inverse. The inverse of the matrix B from question 1 is partially given by
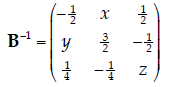
what values of x, y, and z are need to complete the inverse matrix B-1?
| The inverse of a matrix has the following property: BB-1
= 1, or:
To find x, we could not that, from the matrix multiply given above,
Similarly for y and z:
|
6. Hermitian Matrices. What values of x, y, and z will make the
following matrix Hermitian?
(There may be more than one acceptable answer here.)
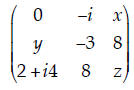
| By inspection, x = 2–i4; y = i, and z = (any real number). |
7. Eigenvalues. Find the eigenvalues (only the eigenvalues!) of the following matrix:
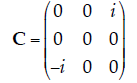
| The eigenvalue equation would look like Cei = ciiei. Solving this
equation, we have:
Given this cubic equation , the possible values of c are c1 = 0, c2 = 1, and c3 = –1. |
8. Eigenvectors of a Hermitian Operator. A suave,
charismatic individual comes up to you
on the street and claims that the following are both eigenvectors of the same
Hermitian
operator:
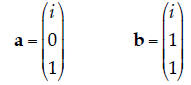
Is it possible the intriguing stranger is telling the truth? Very briefly, why or why not?
| No… the stranger is a dirty liar. All
eigenvectors of a given Hermitian operator are orthogonal to each other, which means that 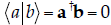 .In
this case, we have .In
this case, we have
So, the two vectors can’t possibly be eigenvectors of a particular Hermitian matrix. |
9. Quadratic Equations . Solve the following equation for x:
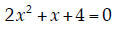
| Using the quadratic formula, we have:
|
10. Logarithms. Find the numerical value of the following logarithm:
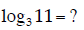
(Show some work so one doesn’t get the false impression your calculator solved all of this !)
On a problem set, you proved that
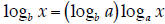 which relates the logarithm of which relates the logarithm ofone base to another. Using this, we can evaluate this logarithm by relating it to another, more common, base. I’ll use the natural base, but base-10 would also work fine:
As a check, we can note that
|
11. Derivatives I. Evaluate the following derivative:
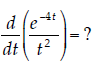
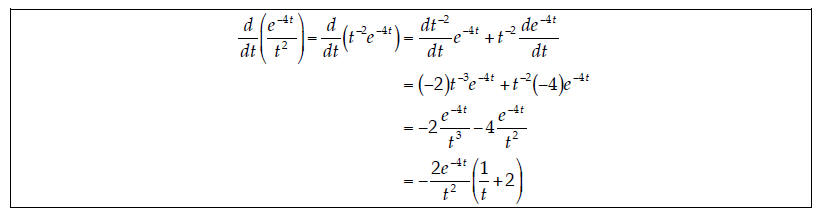
12. Derivatives II. Evaluate the following derivative:
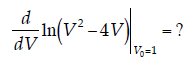
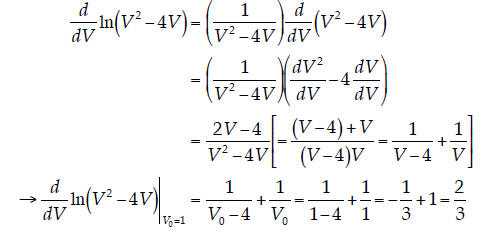 (There’s no need to simplify things further like I did here… it just looks a little prettier that way.) |
Concept Testing. (44 points, 11 points each.) The
following problems are meant to evaluate your
understanding of mathematical ideas. Explain what you are doing… use some
words! Think of it more as
writing a paper than taking an exam. Here, I’ll be looking for evidence of your
mastery of the mathematical
concepts, not so much in getting the right answer. (For many of them, the
“answers” are given!). You may do
these problems in any order.
13. Eigenvalues of Hermitian Operators. Use Dirac
notation to prove that the eigenvalues of
a Hermitian operator are real. Be sure to explain what you’re doing, but be
succinct! There’s
no need for lots of writing.
| We did this one in lecture… see the notes on
9/26/08. Update: Many people
approached this proof the following way, considering the two
Notice that i and j can be different here! So,
we’ll have to do a little more work to show that, Multiply the first equation on the left by
Then, since
Now, because the eigenvectors of Hermitian
operators can be made orthonormal to each other,
…and therefore the eigenvalues of a Hermitian operator must be real. So, you could go this route, but you’d have to
invoke the orthogonality of eigenvectors |
14. Using Dirac Notation. On Exam I, you were asked to show that
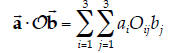
Repeat that proof here using Dirac notation, only
generalize it for the case where the elements
of the matrix O and vectors a and b could be complex numbers. Note that your
answer will
be slightly different because you’re generalizing the proof for complex
elements. [For this
problem, you can use common relations like 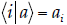 without
proving them; the primary
without
proving them; the primary
objective here is to assess your ability to use Dirac notation.]
In Dirac notation, the left-hand side of the
above equation would be 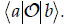 To Tointroduce a basis set, we need to insert the dyadic:
Then, using the fact that
where we have used the fact that
Then, since the ‘adjoint’ of a scalar is simply its complex conjugate, we have:
Note that this result is slightly different, in
that we’d need to use the complex conjugate of the |
15. Logarithms and Inverse Trig Functions. Use what
you know about complex numbers,
logarithms, and inverse trigonometry functions to prove that the logarithm of a
general
complex number (z = x + iy) is given by:
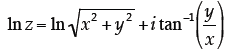
[Hints: You can use the properties of logarithms here
without proving them. You may find
Euler’s formula useful : 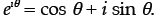 Remember: partial
credit is your friend! If you get
Remember: partial
credit is your friend! If you get
stuck, think logically as far as you can go…]
| There are probably many ways one might approach
this problem. I think I’ll start by writing the general complex number with reference to plane polar coordinates :
Note that
In this form, the original logarithm becomes:
Using the inverse tangent, we can write
And finally, with all these substitutions, we have:
Update: A lot of folks took the brute force
approach to this problem, which is just as
If we focus on the first term in the square brackets , we have:
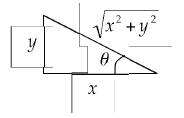
A picture might help evaluate this:
Notice that the angle θ is the result of the
inverse tangent function. I.e. Substituting these results in, we have:
…which is certainly true. Therefore, the original expression must have been true as well! Important: Note that
That’s not how inverse trig functions are defined.
On the left-hand side, the result is an angle.
Instead,
Also Important: Many folks made the following algebra mistake: if ln a = ln b + c,
The actual relation is
It’s also important not to confuse ln b + c with
ln(b + c). If it was really the latter case,
not |
16. The Product Rule. Prove the product rule of derivatives, namely:
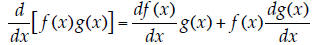
Again: explain your thought process, but be concise!
| We did this one in lecture as well… see the notes on 10/08/08. |
| Prev | Next |
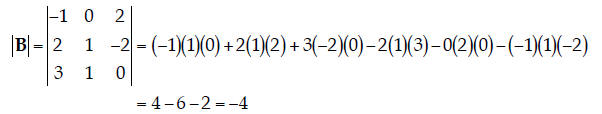
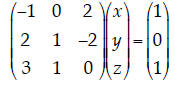
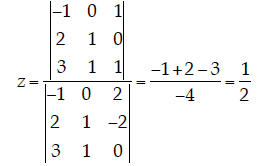
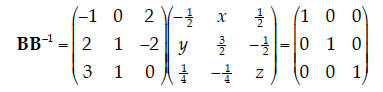
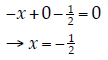
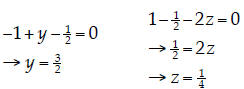
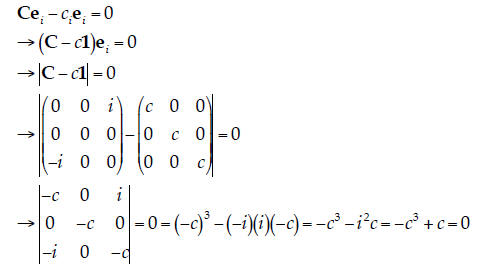
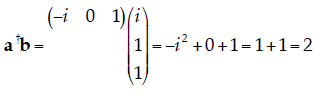
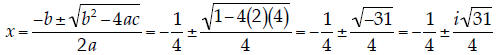
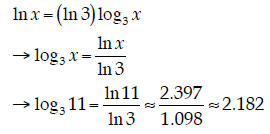
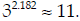

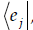 and multiply the second equation on
the
and multiply the second equation on
the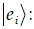
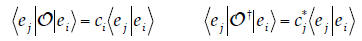
 is
Hermitian, we have
is
Hermitian, we have 
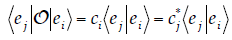
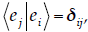 and so we can’t just
and so we can’t just 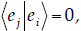 and 0/0 is
undefined. Instead, we can use the Kronecker delta to say that if i ≠ j
and 0/0 is
undefined. Instead, we can use the Kronecker delta to say that if i ≠ j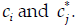 (Indeed, just knowing what one
(Indeed, just knowing what one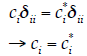
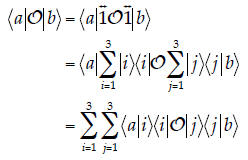
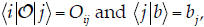 we have
we have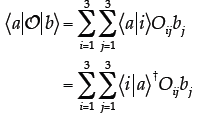
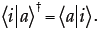 Continuing…
Continuing…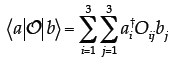
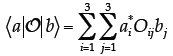
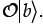

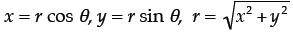 and
and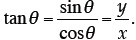 Then, using Euler’s
Then, using Euler’s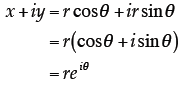
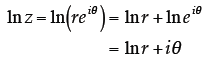
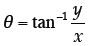
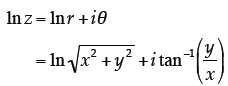
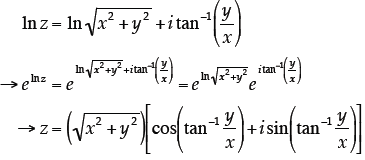
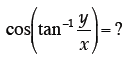
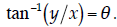 Using
Using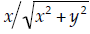 Similarly,
sine of that angle is
Similarly,
sine of that angle is