Math 1314 Chapter 3 Review
1. Graph the parabola whose equations is f (x) = −x2 − 2x
+ 8 . Label the vertex. Also
label one point on each branch of the parabola . Find the y- intercept and any
x-intercepts. State the domain and range of the function.
2. Use synthetic division to find the quotient and
remainder if 2x4 − 3x3 + x2 − 5 is
divided by x + 3.
3. Use synthetic division and the reminder theorem to find
f (-3) if
f (x) = x4 + 2x3 −8x2 +10x − 5 .
4. Use synthetic division and the factor theorem to decide
if x + 3 is a factor of
f (x) = x3 + 4x2 + x − 6 .
5. Find a polynomial function of degree three with real
coefficients having zeros 1, and
2 – 3i, and f (2) = 27.
6. If i is a zero of f (x) = x4 + 2x3 − 7x2 + 2x −8 ,
find the remaining zeros by using
synthetic division.
7. State all the zeros and their multiplicities of :
f (x) = x3 (2x +1)(x − 4)2 (x −1− i)(x −1+ i)
8. Completely factor f (x) = 6x3 + 25x2 − 24x + 5 if -5 is a zero of f (x) .
9. Use Descartes’ Rule of Signs to determine the possible
number if positive and
negative zeros of f (x) = 3x3 −13x2 +17x +15 .
10. Determine if -2 is a lower bound and also determine if
1 is an upper bound for the
zeros of f (x) = 2x3 + 2x2 + 4x + 2 .
11. Find all the zeros of f (x) = 2x3 − 5x2 − 46x + 24
by using the rational zero theorem
and synthetic division.
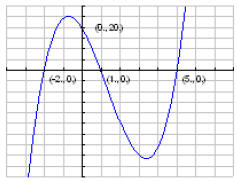
12. Find all the zeros of f (x) = 2x3 −8x2 −14x + 20 by
using the rational zero theorem
and synthetic division and then graph f (x) by labeling the y-intercept, the
xintercepts,
and by determining the end behavior.
13. Use the intermediate value theorem to determine if
there is a zero between 0 and 1
for f (x) = x3 − 4x2 + 2 .
14. Use the intermediate value theorem and synthetic
division to estimate the zero
between x = 3 and x = 4 to the nearest tenth of f (x) = x3 −10x − 3 .
For problems 15 and 16, Graph each rational function by
identifying any
y-intercept, x-intercept(s), and vertical asymptote(s), and horizontal
asymptote, or
any slanted asymptote.
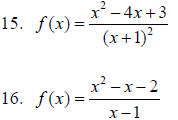
Answer Sheet
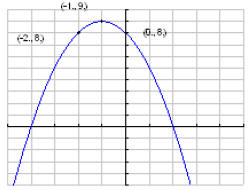
1.
Vertex (-1, 9)
y-int (0, 8)
x-int (-4, 0) (2, 0)
D = (−∞,∞) R = (−∞,9]
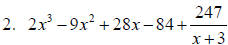
3. f (−3) = −80
4. x + 3 is a factor
5. f (x) = 3(x −1)(x − 2 + 3i)(x − 2 − 3i)
6. Remaining zeros are –i, - 4, 2

8. f (x) = 6(x + 5)(x −1 3)(x −1 2)
9. 2 or no positive zeros , 1 negative zero.
10. -2 is a lower bound, 1 is an upper bound
11. zeros: -4, 1/2 , 6
12. zeros: -2, 1, 5 y-int (0, 20)
13. There is a zero between 0 and 1.
14. 3.3
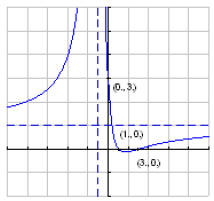
15.
y-int (0, 3)
x-int(3, 0) (1, 0)
Vert. Asym.: x = -1
Horiz. Asym.: y = 1
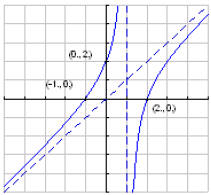
16.
y-int (0, 2)
x-int (2, 0) (-1, 0)
Vert. Asym.: x = 1
Slant Asym.: y = x
| Prev | Next |