Fixed-point Calculator
This laboratory assignment accompanies the book, Embedded
Microcomputer Systems: Real Time Interfacing,
Second edition, by Jonathan W. Valvano, published by Thomson, copyright © 2006.
Goals
• Design and build a calculator,
• Develop routines for fixed- point arithmetic .
Review
• Valvano Section 1.5.5 on fixed-point numbers.
Starter files
• None
Background
You are not required to follow the specific syntax
described in this background section. The two examples
are included to illustrate the approximate level of complexity required of your
calculator. In these examples, an
ASCII string is input from the keyboard. During this input stage, a clear or
backspace key allows the operator to
correct typing mistakes. During the time the operator is entering a new command,
the entire LCD display shows the
command as it is being typed. There will be a specific key or keys (e.g., = ! or
<ENTER>) that terminates the string
and causes the string to be interpreted.
A literal is defined a sequence of characters that
represent a specific value (e.g., 0 1.3 3.14). Operators
are characters (or sequences of characters) that cause actions to occur (e.g., +
- * / 
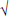= ! A). There may be delimiting
characters, like spaces , which the calculator uses to define its syntax. There
are two basic approaches to building a
calculator. The algebraic approach uses a syntax based on the rules of algebra .
To execute binary operations
(requiring two inputs), we would type the operator between the two inputs
1.3-2.4= (sets the temporary register to -1.10)
30*0.11= (sets the temporary register to 3.30)
Binary operators (+ - * /) can be used in a unary syntax
with the first parameter implied as the temporary register.
For example,
1+2= (sets the temporary register to 3.00)
+3= (sets the temporary register to 6.00)
/8= (sets the temporary register to 0.75)
To execute a unary operation (requiring one input), we would type the operator before the input
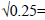(sets the temporary
register to 0.50)
To implement a save register, two functions are needed
(for example, let ! mean store and let A mean recall). The
store function copies the temporary register into the save register, and the
recall function can be used in place of a
literal inside a calculation. For example
1.3+1.7= (sets the temporary register to 3.00)
! (sets the save register to 3.00)
10/A= (sets the temporary register to 3.33)
In this syntax, the = and ! keys cause the line to be
executed . Algebraic calculators use parentheses and operator
precedence to create complex calculations (parentheses and precedence are not
required for this lab). Algebraic
calculators do not need a delimiter, like space, to separate operands. After the
operator hits the = or ! key, your
calculator executes the line and shows both the temporary register and the save
register.
A second approach to implementing a calculator uses
Reverse Polish Notation (RPN), like an HP
calculator. An advantage of RPN is that complex calculations can be performed
without parentheses or operator
precedence rules. The storage elements for a RPN calculator form a LIFO stack.
In this syntax we use the <ENTER>
key to cause a line to be executed. When a literal is executed its value is
pushed on the stack. For example, typing
cause a line to be executed. When a literal is executed its value is pushed on
the stack. For example, typing
1.3 2.4 <ENTER> (pushes 1.30 and 2.40 on the stack, with 2.40 on top)
To execute binary operations (requiring two input), we would type the operator
after the inputs
1.3 2.4 - <ENTER> (pushes a 1.30, pushes a 2.40, pops the 1.30 2.40 and pushes a
-1.10)
To execute a unary operation (requiring one input), we would type the operator
after the input
0.25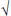 
<ENTER> (pushes a 0.25, pops the 0.25,
then pushes a 0.50 on top of the stack)
RPN calculators will need a delimiter, like space, to
separate operands. Again, two functions are needed to
implement a save register (let ! mean store and let A mean recall). The store
function pops the top element off the
LIFO stack storing it into the save register, and the recall function pushes the
contents of the save register onto the
LIFO stack. For example
1.3 1.7 + ! <ENTER> (sets the save register to 3.00, with
no net change to stack )
10 A / <ENTER> (pushes a 3.33 onto the stack, the save register still contains
3.0)
After the operator hits the <ENTER> key, your calculator
executes the line and shows the top of the LIFO stack and
the save register. Because each token in a RPN calculator always does the same
thing, it will be easy to implement a
calculator that supports multiple operations in one command line. E.g.,
1 2 + 3 + 8 / <ENTER> (pushes a 0.75 on top of the stack)
The RPN interpreter simply scans the string, dividing into tokens (separated by
spaces + - * / )
If the token is a literal, push its value on the stack.
If the token is a binary operator, pop two elements off stack, operate, push
result on the stack.
If the token is a unary operator, pop one element off stack, operate, push
result on the stack.
Preparation
Write the main program that implements a five-function
16-bit signed fixed -point calculator. Your calculator
will have at least two storage variables (e.g., a temporary register and a save
register or a LIFO stack and a save
register). All numbers will be stored using the fixed-point format developed
back in Lab 1. The matrix keyboard
will include the numbers ‘0’-‘9’, and the letters ‘+’, ‘-’, ‘*’, ‘/’, ‘=’ ‘!’
‘A’ ‘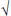’ and ‘.’. (The RPN calculator will also
need a space). You will need either a clear or a backspace character to let the
operator correct typing errors. You are
free to design the calculator functionality in any way you wish, but you must be
able to: 1) observe the save value
and the temporary; 2) type numbers in using the matrix keyboard; 3) add,
subtract, multiply, divide and square root ;
4) display the results on the HD44780 LCD display. No SCI input/output is
allowed in the calculator program.
Figure 10.1 shows a possible data flow graph of the calculator.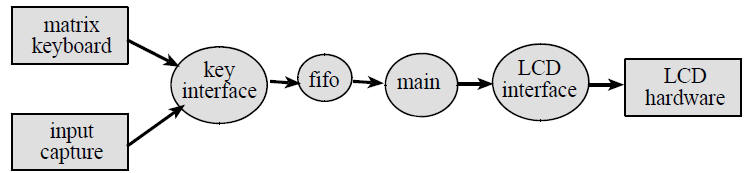
Figure 10.1. Data flows from the keyboard to the LCD.
Figure 10.2 shows a possible call graph of the system.
Dividing the system into modules allows for concurrent
development and eases the reuse of code.
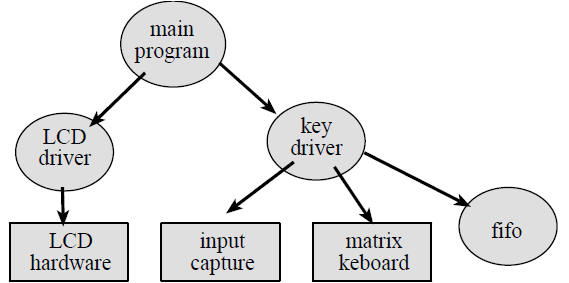
Figure 10.2. A call graph showing the four modules used by the calculator.
Procedure
Test the calculator software in small pieces. You should
stress test the system by purposely attempting illegal or
nonsensical commands. An appropriate response to illegal inputs or improper
syntax is to display an error.
Similarly, the calculator should give a descriptive error after a numerical
overflow, a divide by zero, or a square root
of a negative number . Record the list of test cases and the responses of your
calculator. You could manually type in
the test cases and manually record the responses. Alternatively, you could
create an automated test program, like
Lab 1, that feeds input strings to your calculator and records the output
strings.
Deliverables (exact components of the lab report)
A) Objectives (1/2 page maximum)
B) Hardware Design
Show any changes you made since the previous lab
C) Software Design (a hardcopy software printout is due at the time of
demonstration)
Describe the algorithm you used to calculate square root
Explain any data structures used to implement the calculator
If you organized the system different than Figure 10.1 and 10.2, then draw its
data flow and call graphs
D) Measurement Data
Test log showing input test cases and output responses
E) Analysis and Discussion (1 page maximum)
Checkout
First, the TA will attempt to use your calculator without any verbal
instructions from you at all. You will then
demonstrate any additional functions the TA couldn’t figure out. Be ready to
discuss issues such as range,
resolution, precision, overflow, truncation, roundoff, and dropout.
A hardcopy printout of your software will be given to your TA, and graded for
style at a later time.
Hints
1) Here is a Newton’s Method for finding square root as
defined in floating-point. You can convert this algorithm
into fixed-point. Overflow and dropout should be considered when implementing
fixed-point calculations. Be
careful to make sure the square root function completes, and doesn’t get caught
in an infinite loop. s is the input and
t is the output, such that t will become sqrt(s)
make an initial guess, e.g., t =2.0
do this calculation a small number of times depending on the precision, and the
initial guess (e.g., 8)
t = ((t*t+s)/t)/2
2) Create a half-page instruction sheet, including a key
code layout. This allows you to label the keys without
permanently damaging the keyboard. A good implementation allows the TA, with
just this instruction sheet, to be
able to figure out and use most features of your calculator
| Prev | Next |