Optimization

In this section we will explore the science of optimization. Suppose that you are trying
to find a pair of numbers with a fixed sum so that the product of the two numbers is
a maximum. This is an example of an optimization problem. However, optimization
is not limited to finding a maximum. For example, consider the manufacturer who
would like to minimize his costs based on certain criteria. This is another example of
an optimization problem. As you can see, optimization can encompass finding either a
maximum or a minimum.

Optimization can be applied to a broad family of different functions . However, in
this section, we will concentrate on finding the maximums and minimums of quadratic
functions. There is a large body of real -life applications that can be modeled by quadratic
functions, so we will find that this is an excellent entry point into the study of
optimization.

Finding the Maximum or Minimum of a Quadratic Function

Consider the quadratic function

f(x) = −x² + 4x + 2.

Let’s complete the square to place this quadratic function in vertex form . First, factor
out a minus sign.

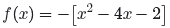
Take half of the coefficient of x and square , as in [(1/2)(−4)]² = 4. Add and subtract
this amount to keep the equation balanced .

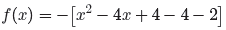
Factor the perfect square trinomial, combine the constants at the end, and then redistribute
the minus sign to place the quadratic function in vertex form.

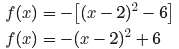
This is a parabola that opens downward, has been shifted 2 units to the right and 6
units upward. This places the vertex of the parabola at (2, 6), as shown in Figure 1.
Note that the maximum function value (y-value) occurs at the vertex of the parabola.
A mathematician would say that the function “attains a maximum value of 6 at x
equals 2.”

Note that 6 is greater than or equal to any other y-value (function value) that occurs
on the parabola. This gives rise to the following definition.

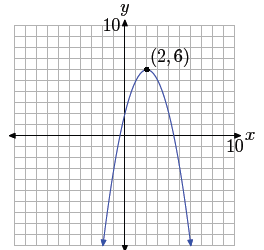
Figure 1. The maximum value of the
function, 6, occurs at the vertex of the
parabola, (2, 6).

Definition 1. Let c be in the domain of f. The function f is said to achieve a
maximum at x = c if f(c) ≥ f(x) for all x in the domain of f.

Next, let’s look at a quadratic function that attains a minimum on its domain.

Example 2. Find the minimum value of the quadratic function defined by the
equation

f(x) = 2x² + 12x + 12.

Factor out a 2.

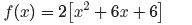(3)

Take half of the coefficient of x and square, as in [(1/2)(6)]² = 9. Add and subtract
this amount to keep the equation balanced.

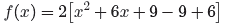
Factor the trinomial and combine the constants, and then redistribute the 2 in the next
step .

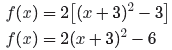
The graph is a parabola that opens upward, shifted 3 units to the left and 6 units
downward. This places the vertex at (−3,−6), as shown in Figure 2. Note that the
minimum function value (y-value) occurs at the vertex of the parabola. A mathematician
would say that the function “attains a minimum value of −6 at x equals −3.

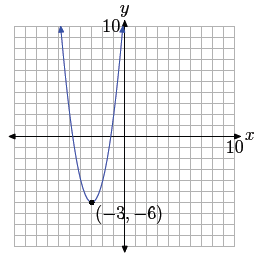
Figure 2. The minimum value of the
function, -6, occurs at the vertex of the
parabola, (−3,−6).

Note that −6 is less than or equal to any other y-value (function value) that occurs on
the parabola.

This last example gives rise to the following definition.

Definition 4. Let c be in the domain of f. The function f is said to achieve a
minimum at x = c if f(c) ≤ f(x) for all x in the domain of f.

A Shortcut for the Vertex

It should now be clear that the vertex of the parabola plays a crucial role when optimizing
a quadratic function. We also know that we can complete the square to find the
coordinates of the vertex. However, it would be nice if we had a quicker way of finding
the coordinates of the vertex. Let’s look at the general quadratic function

y = ax² + bx + c

and complete the square to find the coordinates of the vertex. First, factor out the a.

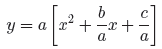
Take half of the coefficient of x and square, as in [(1/2)(b/a)]² = [b/(2a)]² = b²/(4a²).
Add and subtract this amount to keep the equation balanced.

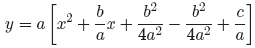
Factor the perfect square trinomial and make equivalent fractions for the constant terms
with a common denominator .

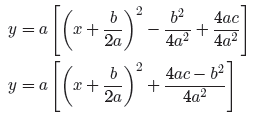
Finally, redistribute that a. Note how multiplying by a cancels one a in the denominator
of the constant term.

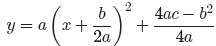
Now, here’s the key idea. The results depend upon the values of a, b, and c, but it
should be clear that the coordinates of the vertex are

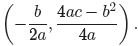
The y-value of the vertex is a bit hard to memorize, but the x-value of the vertex is
easy to memorize.

Vertex Shortcut. Given the parabola represented by the quadratic function

y = ax² + bx + c,

the x-coordinate of the vertex is given by the formula

.
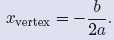
Let’s test this with the quadratic function given in Example 2