What is a Radian

What is a Radian?
Getting Ready

Cultural Knowledge
Mathematics in the Navajo cultural heritage was a learned skilled of estimation from previous experiences. In creating a fork stick Hogan, the person building would estimate the angle of incline of the Hogan based on the type of sand available for use (some sand can be packed without future slump at greater angles). In determining safe hours in working or herding sheep in the hot sun, Navajos used the width of their hands to measure the angle of the sun from the horizon. When the sun was within the first six hand widths from the horizon, it was considered safe to work in the sun. The same type of measurement is true in determining the part of the night by the position of constellations in the night sky.

What is a Radian?
Introduction

Prerequisite :
Lesson: What is a Degree?

Video scene: Students are asked, "What is a Radian?"
Each student has a response.

Student 1: The point between the middle of the circle to the outside of the circle?

Student 2: Umm... I don't know what a Radian is, but... I know what a radius is.

Student 3: Could it be the area outside the circle ? Or around it?

Student 4: Thinking... radius of a circle? Yeah... radius of a circle.

(High School students from Tuba City High School)
Nicole Tsingine, Crystal Dugi, Jose Dastas, Rhonda Yazzie, Delewis Daw,
Deidra Dogsleep

What is a Radian?
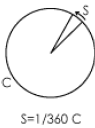
Circumference

We’ve learned that there are a total of 360º in a circle and that each degree has an arc length ‘s’ that is 1/360th of the circle’s circumference.

From previous lessons in mathematics , we also know that the circumference of a circle ‘C’ is equal to π (pi) times the diameter ‘d’.
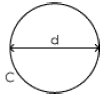C=dπ
We know too that the diameter of the circle is twice as long as the radius of the circle.
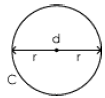d=2r
So we can say that the circumference of a circle is also equal to π (pi) times 2 times the radius ‘r’. Or, we can say that the circumference is equal to 2 times π times the radius ‘r’.
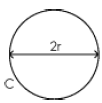C=2rπ or C=2πr

What is a Radian?
Radian

Now, let’s give the radius a value equal to one.
Which makes the circle’s diameter equal to 2.

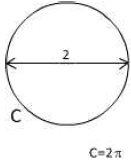
r=1 d=2r d=2
That means the total distance around the circle is 2π or approximately 6.28.
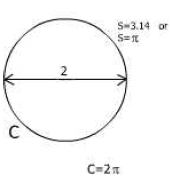C=2π C=6.28
Divide each arc length as follows.

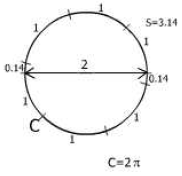
When the arc length is equal to 1, the angle that it makes is called 1 radian or 1 rad.

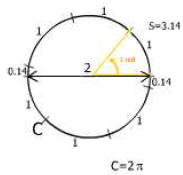
This angle is 2 rad (read as two radians ).

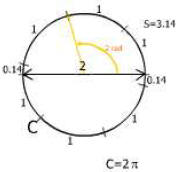
This angle is 3 rad (read as three radians).

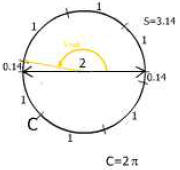
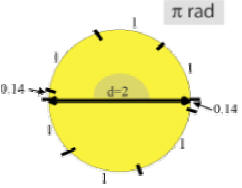
This angle is π rad (or 3.14 radians).

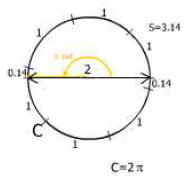
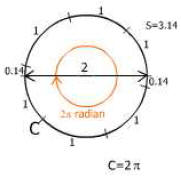
The full circle has an angle of 2 rad (read as two pi radians).

Name: ______________________________
Angles Activity
What is a Radian

Classify and measure the angles in degrees and radians.

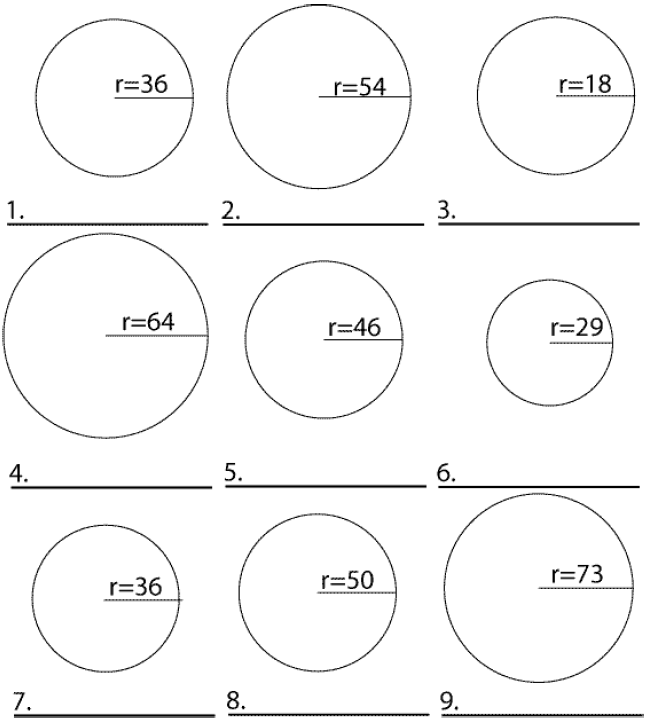
Find the circumference of each circle.

What is a Radian?
Activity

Give the measure in radians for the following angles in the space provided.

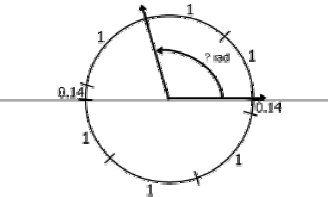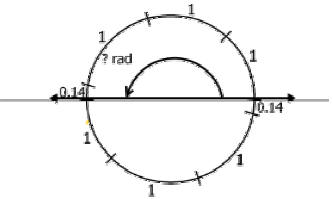Diagaram 1.	Diagram 2.
	Hint1: Remember that half of the circle has an arc length of Pi (or approximately 3.14)
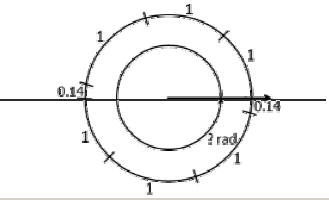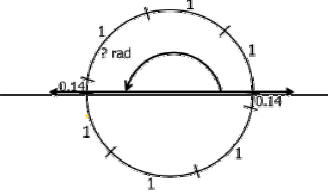Diagram 3.	Diagram 4.
Hint2: What would the arc length of a full circle have ?	Match correct answer with correct Diagram:
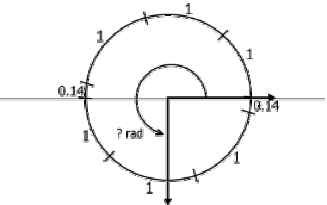	a. π radian b. 2 radian c. - 2 radian d. - π/2 radian e. 2 π radian
Diagram 5.
Hint3: If half of a circle has an arc length of Pi (or approximately 3.14), what might a quarter of a circle’s arc length be? Also, remember the direction of rotation.

What is a Radian?
Glossary

Arc - a section of a continuous curve such as the circle
Circumference - the total distance around the outer edge of a circle.
Diameter - the distance across a circle going through the center of the circle
Degree - the unit of measure for measuring angles derived from the angle that a section of one of 360 equal 'pies' of a circle makes.
Pi (π ) - a symbol that represents the constant ratio of the circumference of a circle to the its diameter having a value of 3.141592654
Radius - the distance from the center of a circle out to the edge of a circle (usually half of the diameter of a circle)
Radian - unit of measure for measuring angles derived from the angle that a section makes when a circle with a circumference value of 1 and an equal arc length
What is a Radian?

What is a Radian?
Digging Deeper

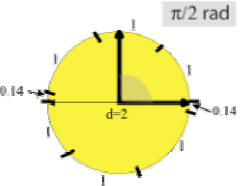
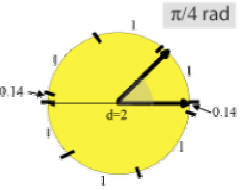
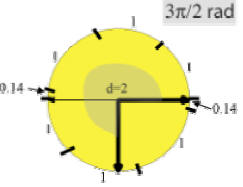
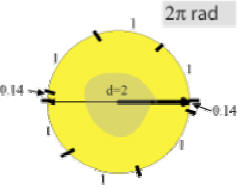
Observe the pattern of each of the angles given in π radians.

These are special angles that you will need to become familiar with for the trig functions in the future.

What is a Radian?
Conclusion

Video scene: Students are asked, "What is a Radian?" again.
each student has a different response .

Student 1:a unit of measure for measuring angles
Student 2:derived from the angle...
Student 3:section of a circle with a circumference
Student 4: value of one and an equal arc length

(High School students from Tuba City High School)
Nicole Tsingine, Crystal Dugi, Jose Dastas, Rhonda Yazzie, Delewis Daw, Deidra Dogsleep
Copyright 2003 NETC