Math Exam 2 Answers
1. Explain in detail how you would find the t curve
using techniques of this
course. (Warning: To check your answer, you might want to make up four data
points and work out the solution explicitly .)
Answer: We want to solve
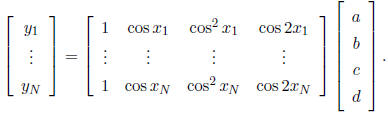
Let A denote that big N ·4 matrix made from the xi. From
our discussion of least squares we
know that if A has rank 4, then AT>A is invertible and the least
squares solution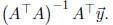
However, our A is not of rank 4, because the set of functions
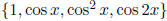 is not
is not
linearly independent ! For example,
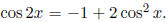 So let's throw out the cos 2x term.
So let's throw out the cos 2x term.
Now we want to solve

The procedure is to let A be that big N ·3 matrix (which
is of rank 3, as needed) and compute
the least squares solution as
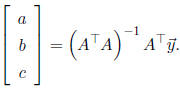
This gives us the coefficients a , b, c to use in the t
curve
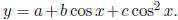 This function
This function
satisfies the requirements of the problem, because it is of Ms. Ogunmola's
requested form with
d = 0.
[Remark: I expected that most students would not realize that the four functions
are not
independent. That is why I suggested working an example; in any example it
becomes clear
that AT>A is not invertible (although it may not be clear how to x
this).]
[Remark: Instead of throwing out cos 2x we could throw out 1 or cos2
x. We could not throw
out cos x without truly making our wind speed model less expressive.]
2. Show that if 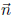 is perpendicular to a
given polygon, then
is perpendicular to a
given polygon, then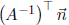 is perpen-
is perpen-
dicular to the transformed polygon.
Answer: Let 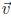 be any vector lying in the
transformed polygon. We wish to show that
be any vector lying in the
transformed polygon. We wish to show that
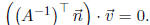 Toward that end, let
Toward that end, let
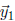 and
and 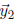 be the
points at the head and tail of
be the
points at the head and tail of
![]() , so
, so
that 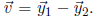 These points
These points![]() and
and
![]() are in the transformed
polygon, so there must exist
are in the transformed
polygon, so there must exist
points ![]() and
and
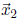 in the original polygon such that
in the original polygon such that
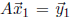 and
and 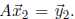 Because
Because 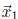 and
and
![]() are points in the
original polygon,
are points in the
original polygon,
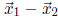 is a vector lying in the original polygon,
and so
is a vector lying in the original polygon,
and so
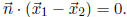 Then, using the basic facts that
Then, using the basic facts that
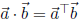 and
and 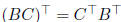 , we
have
, we
have

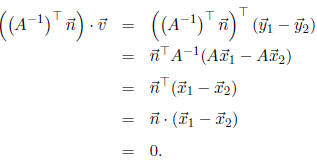
3. What happens in the special case when A is a
rotation? Explain in detail.
Answer: If A is a rotation, then A preserves the length of any vector, so A
is orthogonal.
This implies that 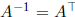 , so that
, so that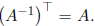 In this special case, normals transform by
In this special case, normals transform by
A. This makes sense, because an orthogonal transformation such as a rotation
preserves angles ;
if ![]() is perpendicular
to a polygon, then after both are transformed orthogonally the results will
is perpendicular
to a polygon, then after both are transformed orthogonally the results will
still be perpendicular.
4. Using only the definitions of trace and matrix multiplication, prove that
for
any two matrices A and B,
tr (AB) = tr (BA):
Answer: For any n · n matrices A and B,
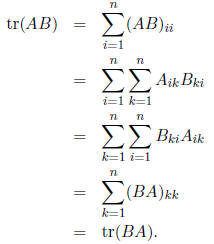
5. Using Problem 4, prove that for any matrix C and any
invertible matrix S,
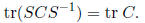
Answer: Let A = S and B = CS-1. Then, using
Problem 4,
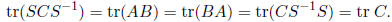
6. Prove that B is really a basis for 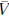 .
.
Answer: First we show that
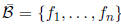 is linearly independent . Suppose that
is linearly independent . Suppose that
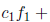
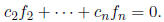 Apply this function to v1:
Apply this function to v1:
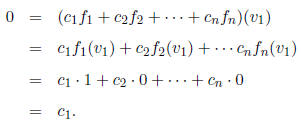
So c1 = 0. Similarly, applying the function to
any vj
shows that cj = 0. Thus 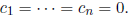
This shows that B is linearly independent . To show that it spans
![]() , let f :
, let f :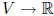 be an arbitrary
be an arbitrary
linear transformation . Let 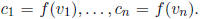 I claim that
I claim that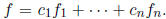 To
To
see this, let vj be any element of B. Then
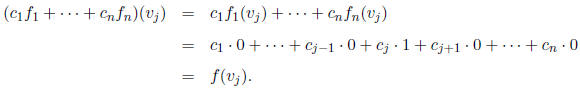
So the functions 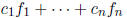 and f
agree on every element of B, and hence on all of V .
and f
agree on every element of B, and hence on all of V .
7. What is the relationship between 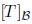 and
and
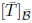 ?
?
Answer: In order to simplify the notation, let
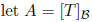 and
and 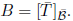 These mean that
These mean that
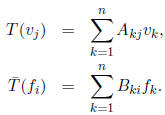
We now compute 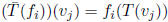 in two
different ways . On the one hand,
in two
different ways . On the one hand,
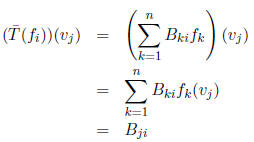
(because only the k = j term survives ). On the other hand,
using the fact that fi is linear we
have
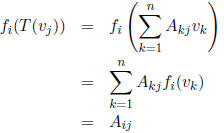
(because only the k = i term survives). Thus
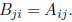 We conclude that
We conclude that
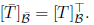
[Remark: Some students were skeptical of this problem; they seemed to suspect
that I made
it up just to irritate them! I did not; the dual space (I substituted the term
\mirror space" to
throw o potential cheaters) is a foundational concept used throughout linear
algebra and its
applications. For example, you can't do general relativity without it.]
[Remark: Remember that matrices are used to represent linear transformations
(among other
things). Multiplying matrices corresponds to composing transformations; that's
why matrix
multiplication exists. Adding matrices corresponds to adding transformations. So
to what does
transposing matrices correspond? Now you know: dualizing transformations.]
| Prev | Next |