Math Homework 2 Solutions
Exercise T1.7: Find the period-two orbit of G(x) = 4x(1 −
x).
Solution : We know from earlier work that G(x) has the fixed points x = 0
and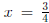 
. Now, we solve G 2(x) = x which means G(G(x)) = x. But,
G(x) = 4x − 4x2 and so G(G(x)) = 16x − 80x2 + 128x3 − 64x4 = x.
=> 15x − 80x2 + 128x3 − 64x4 = 0. Using synthetic division we get, x(x −
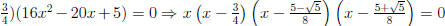. This means
that the period- two fixed points are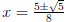 
, and
hence the period- two orbit
is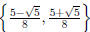 
.
Exercise T1.11: Construct the periodic table for f in Example 1.9 (follow
the form given by Table 1.3).
Solution: The map is f(x) = 3x( mod 1) on the unit interval.
| Period k |
# of fixed points of fk |
Divisors of k |
# of fixed points of fk due to lower period orbits |
Orbits of period k |
 |
||||
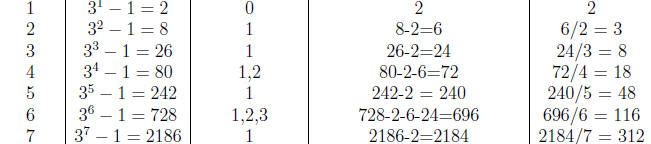Exercise T1.12: Consider the 3x mod 1 map of the unit
interval [0,1].
Define the distance between a pair of points x, y to be either |x − y| or
1−|x−y|, whichever is smaller. (We are measuring with the ” circle metric ”,
in the sense of Figure 1.11, corresponding to the distance between two points
on the circle .) (a) Show that the distance between any pair of points that lie
within 1/6 of one another is tripled by the map. (b) Find a pair of points
whose distance is not tripled by the map. (c) Show that to prove sensitive
dependence for any point, d can be taken to be any positive number less than
or equal 1/2 in Definition 1.10, and that k can be chosen to be the smallest
integer greater than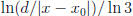 
.
Solution: We start with part c. We need to show that
.
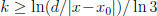Let x and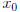 
be given, also let f be the map 3x mod 1. From definition 1.10
we have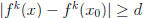
for some positive distance d. Apply the definition
to the map and note that if f(x) = 3x mod 1, then fk(x) = 3kx mod 1
to get,
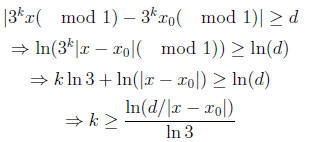
Now we are investigating
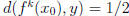for some k.
Let’s consider some
neighborhood around 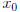of radius 2ε where
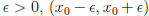. k depends
on ε, i.e. after some k iterations we will find a point y for which the map
covers the whole circle and not just that but also
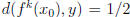. Here,
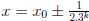. To prove this consider,
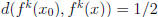
To do part a, note that
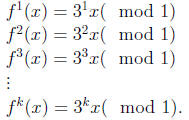
Case 1, we need to show that if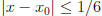 
, then the
distance between x
and 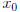triples after the first iteration. Consider,
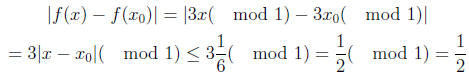
i.e. the distance between x and 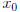is being tripled.
Case 2, similarly if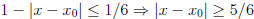 
, then
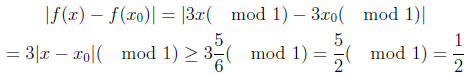
i.e. the distance between x and 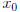is being tripled.
To answer part b, take x = 1/6 and y = 1/2. |x − y| = 1/3, however,
|f(x) − f(y)| = |3(1/6)( mod 1) − 3(1/2)( mod 1)| = |1/2 − 1/2| = 0, not
tripled!
Exercise T1.14a: Find a point that lies in the subinterval LLR.
Solution: Given G(x) = 4x(1−x). To find the a point that lies in the subinterval
LLR, we first need to find the endpoints ”cut off points” that give this
subinterval, then any point that belongs to this subinterval will work. The
solution
to the equations G (x) = 1/2 and G2(x) = 1/2 will give those endpoints,
however, we need to keep in mind that these equations will give several answer
for which we are interested only in the ones that give LLR itinerary. Now
solving G (x) = 1/2 provides the solution set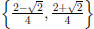 
,
and G2(x) = 1/2
provides the solutions set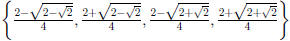 
. Hence,
the subinterval of [0,1] that gives LLR is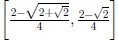 
.
For example, take
x = 0.1.
Exercise E1.5: Is the period-two orbit of the map f(x) =
2x2 − 5x on R a
sink, a source, or neither.
Solution: First note that the period-two orbits of f(x) consist of the points
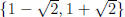. Also, the fixed points of this map are x =
0 and x = 3,
from previous work . Now to test whether the period-two orbit is a sink, a
source, or neither, we need to evaluat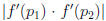e 
where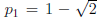 
and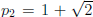 
. Differentiating f (x) gives f'(x) = 4x −
5. So, 
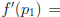
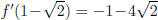and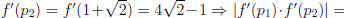 
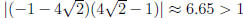. Since, 
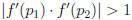the period-two
orbit of f(x) = 2x2 − 5x on R is a source.
| Prev | Next |