Mathematics Practices
Exploration 15-1a: Cubic Function Graphs
Objective: Learn the shape and some properties of cubic function graphs.
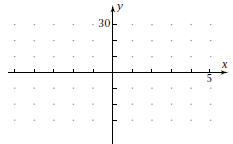
1. Let 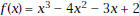 Plot the graph using a Plot the graph using awindow with x-range of about [-5, 5] and a y-range of [-30, 30]. Sketch the graph.
2. The graph in Problem 1 crosses the x-axis at
three 3. The integer value in Problem 2 can be used to
write a 4. With the help of the quadratic formula , find
the 5. Let |
6. Factor  into three linear factors .
By setting each into three linear factors .
By setting eachfactor equal to zero, find the three x-intercepts. What do you notice about two of the x-intercepts?
7. Let 8. Find one linear factor of
9. What did you learn as a result of doing this
|
Exploration 15-2a: Synthetic Substitution
Objective: Learn how to evaluate f(x) quickly by
pencil and paper and how to use
the result to factor f(x).
1. Let 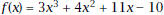 Plot the graph using a Plot the graph using awindow with an x-range of about [-5, 5] and a y-range of [-100, 100]. Sketch the graph here.
2. Find 3. Use long division to divide
4. What do you notice about the remainder and the |
6. How could you write the answer to Problem 3 directly from the synthetic substitution results ?
7. Find 8. Use the result of Problem 7 to find the other
two 9. What did you learn as a result of doing this
|
Exploration 15-2b: Sum and Product Date:
of the Zeros of a Polynomial
Objective: Discover properties relating the sum and
the product of the zeros of a
polynomial function.
| The figure shows the graph of
1. Find 2. Find the product of the zeros,
3. If you factor out 5 from each term in the
equation of
How does the product of the zeros you found in 4. Find the sum of the zeros,
|
5. Find the sum of the pairwise products of the
zeros,
How does the answer relate to the coefficients in 6. Use the patterns you observe in Problems 1–5 to
find
7. Find the particular equation of the cubic
function 8. Plot the graphs of g and h on the same screen.
Do 9. What did you learn as a result of doing this
|
Exploration 15-3a: Fitting a Polynomial Date:
Function to Points
Objective: Given a set of points, find the
particular equation of a polynomial
function that fits the points.
|
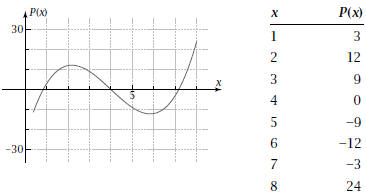
The figure shows the graph of a polynomial function P. The table shows plotting points for this function.
1. Show that the third differences between the
Find the particular equation of the cubic function 3. Show that the equation of Problem 2 fits the
other |
4. Find the particular equation of Problem 2 again, using the cubic regression feature of your grapher. Does the equation come out the same? What statistic tells you that the fit is perfect ? 5. Use
your equation to predict the value of P(20). P(x) = (x - 4)(other factor)
|
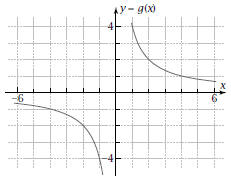
Exploration 15-4a: Rational Functions Date:
and Discontinuities
Objective: Find and classify discontinuities in the graph of a rational algebraic function.
|
1. On this graph paper, plot quickly the graph of the rational function 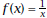 (no grapher). (no grapher).
|
5. Function r is called a rational function because
equals a ratio of two polynomials.
10. What did you learn as a result of doing this
|
| Prev | Next |
 . By
. By 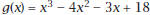 Plot
the graph of g on
Plot
the graph of g on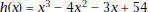 Plot the
graph of h.
Plot the
graph of h.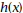 . Use it to find two other
. Use it to find two other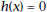 How do the
results
How do the
results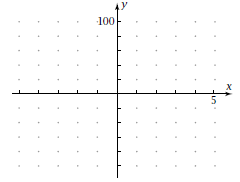
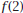 . Mark
the corresponding point on your
. Mark
the corresponding point on your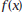 by
by
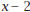 See
See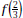 by
synthetic substitution. How does the
by
synthetic substitution. How does the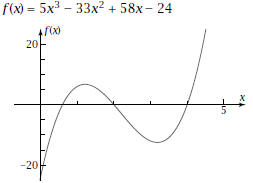
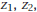 and
and
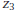 the three zeros of this function.
the three zeros of this function.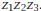
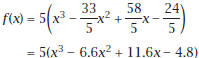
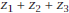 .How does the
.How does the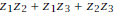
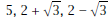
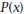

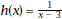 What transformation of the
graph of f
What transformation of the
graph of f
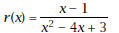
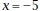 to
to
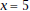 that includes each
that includes each
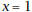 . Explain algebraically why there is
a
. Explain algebraically why there is
a