Problem Type 2 Solving Equations

The problem of factoring and the problem of solving are linked by the Zero Property of
Equality :

Important Idea (Zero Property of Equality). For any real numbers a and b,

ab = 0 means either a = 0 or b = 0:

In essence, this says that the only way to multiply two real numbers together to get 0 is
for at least one of the numbers to be zero. So if you have an equation already in factored
form such as

(x + 3)(x - 4) = 0

then you have one number (actually an expression representing a number), x+3 multiplying
a second number (again an expression) x - 4 whose product is zero . Thus, the only way for
this to happen is for one of them to have been zero. This means to solve it, we simply set
each factor equal to zero and solve .

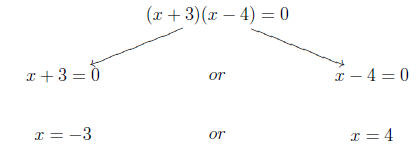
This works well until we are given a problem which is not in factored form. Then the strategy
becomes as follows.
(a) Transform the equation into an equivalent equation of the form

ax² + bx + c = 0:

(b) Solve the equation using the Quadratic Formula .

(i) Compute the Discriminant, D.
(ii) Use the formulas

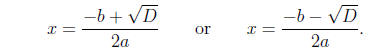
In this case the discriminant tells use if we will have one solution, two solutions , or no
solutions. Actually when we say no solutions, we really mean that the solutions are non -real
complex number solutions , but more about that later.

Important Idea. Notice the major di erence in solving and factoring is that when we solve,
there is no need to transform the roots into a factor .

Example 9. Solve the equation 6x² - 5x + 1 = 0.
Solution. Since the equation is in the proper form, expanded and set equal to zero, we just
identify a, b, and c

a = 6, b = -5, , c = 1.

Computing the discriminant

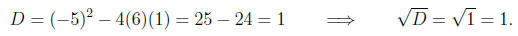
Thus, for the solutions

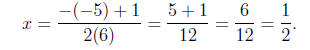
or

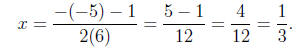
Thus, the solutions are

x =1/2 or x =1/3.

Example 10. Solve the equation x² - x = 12.
Solution. Since the equation is not set to zero on one side, we transform by subtracting 12
on both sides.

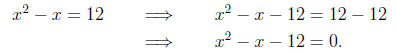
Now we can identify a, b, and c, so that

a = 1, b = -1, c = -12.

Computing the discriminant

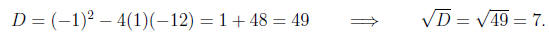
Computing the roots

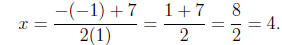
or

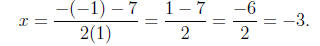
Thus, the solutions are

x = 4 or x = -3.

Checking this we see

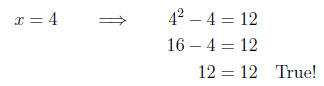
and for the second solution

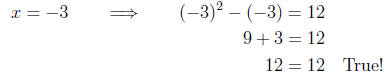
Example 11. Solve the equation 6x² - 20x = 3x - 20.
Solution. Once again, we need to have it in the correct form to apply the Quadratic formula.
Moving the 3x - 12 to the opposite side, we have

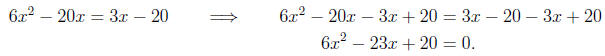
Now determining a, b, and c

a = 6, b = -23, c = 20.

Computing the discriminant

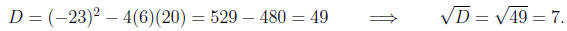
Computing the roots

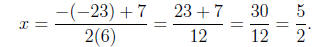
or

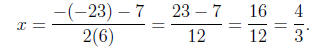
Thus, for our solutions

x = 5/2 or x =4/2.

Example 12. Solve the equation (x - 3)(x + 1) = 32.
Solution. Warning! Even though the left side looks like it is factored, we can't just set each
factor equal to 12 and solve. We need one side to equal zero. Therefore, we have some
expanding to do.

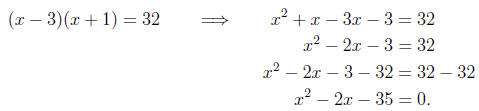
Now we are ready to identify a, b, and c

a = 1, b = -2, c = -35.

Computing the discriminant

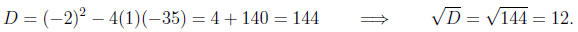
Computing the roots
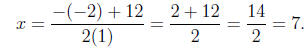2
or
:
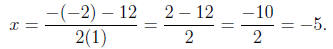Thus, the solutions are
x = 7 or x = -5.