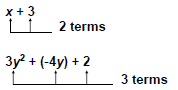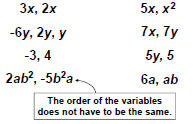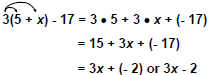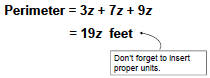Solving Equations and Problems Solving

Section 3.1

Simplifying Algebraic
Expressions

In algebra letters called variables
represent numbers.

The addends of an algebraic expression are
called the terms of the expression.

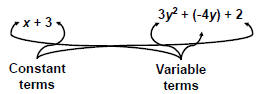
A term that is only a number is called a constant
term, or simply a constant. A term that contains
a variable is called a variable term.

The number factor of a variable term is called the
numerical coefficient . A numerical coefficient of
1 is usually not written.

Terms that are exactly the same, except that they
may have different numerical coefficients are
called like terms .

Like Terms	Unlike Terms

A sum or difference of like terms can be
simplified using the distributive
property.

Distributive Property

If a, b, and c are numbers, then

ac + bc = (a + b)c

Also,

ac - bc = (a - b)c

By the distributive property,

7x + 5x = (7 + 5)x

= 12x

This is an example of combining like terms .

An algebraic expression is simplified when all
like terms have been combined.

The commutative and associative
properties of addition and multiplication
help simplify expressions.

Properties of Addition and Multiplication

If a, b, and c are numbers, then

Commutative Property of Addition

a + b = b + a

Commutative Property of Multiplication

a · b = b · a

The order of adding or multiplying two numbers
can be changed without changing their sum or
product .

The grouping of numbers in addition or
multiplication can be changed without
changing their sum or product.

Associative Property of Addition

(a + b) + c = a + (b + c)

Associative Property of Multiplication

(a · b) · c = a · (b · c)

Examples of Commutative and Associative Properties
of Addition and Multiplication

4 + 3 = 3 + 4	Commutative property of Addition

6 · 9 = 9 · 6	Commutative property of Multiplication

(3 + 5) + 2 = 3 + (5 + 2)	Associative property of Addition

(7 · 1) · 8 = 7 · (1 · 8)	Associative property of Multiplication

We can also use the distributive property
to multiply expressions.

The distributive property says that
multiplication distributes over addition
and subtraction.

2(5 + x) = 2· 5 + 2 · x = 10 + 2x

or

2(5 – x) = 2· 5 – 2 · x = 10 – 2x

To simply expressions, use the distributive
property first to multiply and then combine
any like terms.

Simplify: 3(5 + x) - 17

	Apply the distributive property
	Multiply
	Combine like terms

Helpful Hint

3 is not distributed to the -17 since
-17 is not within the parentheses .

Finding Perimeter

Perimeter is the distance around the figure.

Finding Area

Don’t forget . . .

Area:
• surface enclosed
• measured in square units

Perimeter:
• distance around
• measured in units