Factoring Special Products

Perfect Square Trinomials

In order for a polynomial to be a perfect square
trinomial , two conditions must be satisfied:

1. The first and last terms must be perfect squares.

2. The “ middle term ” must equal 2 or – 2 times the
product of the expressions being squared in the
first and last term.

Example: Factor the following :

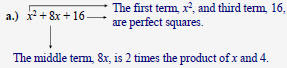
x² + 8x + 16 = (x + 4)²

b.) 9x⁴ − 30x²z + 25z²

9x⁴ − 30x²z + 25z² = (3x² – 5z)²

The Difference of Two Squares

Example: Factor the following :

a.) 3x² − 27
3x² − 27 = 3(x² – 9)  3 is a common factor.
= 3(x + 3)(x – 3)
 

b.) 4x² − 25y⁴
4x² − 25y⁴ = (2x + 5y²)(2x – 5y²)

The Sum of Two Cubes

Example: Factor: 27x³ + 125
a = 3x
b = 5

27x³ + 125 = (3x)³ + 5³
= (3x + 5) [(3x)² − 3x·5 + 5²]
= (3x + 5)(9x² − 15x + 25)

The Difference of Two Cubes

Example: Factor: x³ − 64
a = x
b = 4

x³ − 64 = x³ – 4³
= (x − 4) (x² + 4x + 4²)
= (x − 4) (x² + 4x + 16)

Practice

Factor each perfect square trinomial completely

x² + 14x + 49

x² − 8x + 16

4a² − 12ab + 9b²

4x² + 20x + 25

n² − 16

a⁴ − 16

36 p² − 49q²

9x⁶ − 25y⁸

64x³ + 1

8x³ − 27

4x⁴ − 4xy³

125a⁶ + 8b³