Math 554 Lecture Note Set 1
Defn. From the introductory lectures, an ordered set is a set S with a
relation ‘<’ which satisfies
two properties :
1. (Trichotomy property) for any two elements a, b ∈ S, exactly one of the following hold
a < b, a = b, or b < a.
2. (Transitive property) for any three elements a, b, c ∈ S, if a < b and b <
c, then a < c.
In this case the relation ‘<’ is called an order.
Defn. Suppose that S is an ordered set and A
⊆ S. An element β ∈ S is
said to be an upper bound
for A if
a ≤ β, ∀a ∈ A.
An element α is said to be a least upper bound for A if
1. α is an upper bound for A
2. if β is any upper bound for A, then α ≤ β.
In this case, the supremum of A (=: supA) is defined as α. The definitions
are similar for lower
bound, greatest lower bound and inf A, respectively. Note that we have already
shown that the least
upper bound (for a nonempty set bounded from above) is unique.
Defn. A set S is said to have the least upper bound property if each
nonempty subset of S which is
bounded from above, has a least upper bound.
Theorem. Suppose the ordered set S has the least upper bound property,
then it has the greatest
lower bound property (i.e. each nonempty subset of S which is bounded from below
has a greatest
lower bound).
Proof. Suppose that a nonempty set A has a lower bound, call it ℓ. Define L
as the set of all lower
bounds of A, then L is nonempty (ℓ ∈ L). Observe that each member of the
nonempty set A is
an upper bound of L so by the least upper bound property, L has a least upper
bound. Call this
element α.
First observe that α is a lower bound for A. Otherwise, there exists an
element b ∈ A with
b < α, but each element of A is an upper bound for L, so this element b is an
upper bound of L
which is smaller than α, the least upper bound of L. This would be a
contradiction. Therefore,
α ∈ L.
Also, if ℓ is any lower bound of A, then ℓ ≤ α since α = sup L. Hence α is
the greatest lower
bound of A.
Defn. The real numbers are defined to be a set IR with two binary operations
(+, ·) which satisfy
the following properties: Given any a, b, c in IR
1. a + (b + c) = (a + b) + c.
2. a + b = b + a.
3.
∃0 ∈ IR 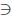 a + 0 = a,
∀a ∈ IR.
a + 0 = a,
∀a ∈ IR.
4. for each a ∈ IR,
∃(−a) ∈ IR, so that a + (−a) = 0
5. a · (b · c) = (a · b) · c.
6. a · b = b · a.
7.
∃1 ∈ IR 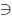 1 ≠ 0 and a · 1 = a,
∀a ∈ IR.
1 ≠ 0 and a · 1 = a,
∀a ∈ IR.
8. for each a ∈ IR with a ≠ 0,∃a-1 ∈ IR, so that a · a-1 = 1.
9. a · (b + c) = (a · b) + (a · c).
(Note: These properties just say that IR is a nontrivial field.)
Moreover, there is a distinguished subset IP (the positive cone ) of IR with
the following proper-
ties: Given any a, b in IP,
a. a + b ∈ IP,
b. a · b ∈ IP,
c. For each a in IR, exactly one of the following properties holds:
i) a ∈ IP,
ii) −a ∈ IP,
iii) a = 0.
Finally, IR must satisfy the least upper bound property, that is, each
nonempty subset of IR
which has an upper bound has a least upper bound. These terms are defined
shortly.
Defn. For the real numbers, define a < b as b − a ∈ IP
Lemma. Using the field properties of IR, the following properties hold
and are all assigned home-
work problems (see p. 3 of this lecture set):
(1) The additive and multiplicative identities are unique.
(2) The additive and multiplicative inverses are unique.
(3) If a ∈ IR, then a · 0 = 0.
Theorem. The positive cone IP induces an order on the real numbers,
i.e. IR equipped with the
relation ‘<’, is an ordered set.
Proof. Assigned homework Problem 2.5.
Notation:
‘b − a’ is defined as b + (−a).
‘a ≤ b’ means either a < b or a = b.
The fraction ‘ a/b ’ means a · b-1.
Lemma. For each a, b, c ∈ IR,
(i.) (−a) = (−1) · a.
(ii.) 0 < 1.
(iii.) if 0 < a, then (−a) < 0.
(iv.) if a < b and 0 < c, then a · c < b · c.
(v.) if a < b, then a + c < b + c.
(vi.) if 0 < a, then the multiplicative inverse of a is positive, i.e. 0 < a-1.
(vii.) the product of two negative real numbers is positive, while the product
of a negative real
number and a positive real number is negative .
Proof. Since
a + ((−1) · a) = (1 · a) + ((−1) · a) = a · (1 + (−1)) = 0 · a,
it follows from the fact that a · 0 = 0 (Homework Problem 2.4) that α := (−1)
· a is an additive
inverse for a. But additive inverses are unique (from your Homework Problem
2.2), so the conclusion
of part (i) follows.
To prove part (ii), we assume to the contrary, i.e. that
 .
By the definition, 1 ≠ 0, so
.
By the definition, 1 ≠ 0, so
(−1) ∈ IP and therefore 0 < −1. But (−1) · (−1) = −(−1) = 1 by part (i) and the
HW Problem
that additive inverses are unique. This shows that 1 ∈ IP by property (b) of the
positive cone and
the assumption that (−1) ∈ IP. Contradiction, by the trichotomy property (c).
For part (iii), observe that 0 < a means a ∈ IP. Since additive inverses are
unique, then
−(−a) = a, and so (0 − (−a)) = −(−a) = a ∈ IP. This is equivalent to the
statement (−a) < 0.
To prove (iv), use the definition of < to show both b − a and c are in IP.
The positive cone is
closed under multiplication, so (b−a)c ∈ IP. Using the property (i) shows then
that (bc)−(ac) ∈ IP
and so ac < bc.
Property (v), is proved similar to showing that 0 < 1. Indeed, suppose that b
:= a-1 < 0, then
−b is positive and so −1 = (−b) · a is positive. Contradiction, since −1 is
negative.
The proof of property (vi) is left for additional practice.
Lemma. Suppose that A is a nonempty subset of IR, with least upper
bound M, then for every
ε
> 0, there exists a ∈ A such that
M −
ε < a ≤ M.
Proof. Since 0 <
ε,
then M −
ε
< M. This shows that M −
ε
cannot be an upper bound for A.
Hence there is a member of A, call it a, so that M −
ε
< a.
Theorem. (Archimedean Property) Suppose a, b are positive real numbers, then
there exists
n ∈ IN such that b < n · a. (Here IN is the set of natural numbers, i.e. 1 and
all its successors,
1, 1 + 1, 1 + 1 + 1, . . .).
Proof. Suppose to the contrary that na < b for all n ∈ IN, then it follows
that α := b/a is an upper
bound for the natural numbers. Let M be the least upper bound. By the lemma, 1/2
> 0, so there
exists a natural number N so that M − 1/2 < N. But then, M < N + 1/2 < N + 1,
which shows
that M is not an upper bound for IN. Contradiction.
Corollary. The natural numbers IN are not bounded.
Corollary. Given any ε > 0, there exists n ∈ IN such that 0 < 1/n < ε.
Homework #2 (Due Tuesday Sept 9.)
1. Show that the additive (or multiplicative) identity is unique.
2. Show that additive (or multiplicative) inverses are unique.
3. Prove that −(a + c) = (−a) + (−c).
4. Prove that a · 0 = 0 for each a in IR.
5. Prove that ‘<’ is an order for IR.
6. Prove that a < b and c < 0 implies that b · c < a · c.
7. Prove that if 0 < a < b, then 0 <1/b<1/a
Notation: Next we define intervals of real numbers.
(a, b) := {x ∈ IR|a < x < b} is called the open interval with endpoints a, b.
[a, b] := {x ∈ IR|a ≤ x ≤ b} is called the closed interval with endpoints a, b.
(a, b] := {x ∈ IR|a < x ≤ b} and [a, b) := {x ∈ IR|a ≤ x < b} are called the
half open intervals with endpoints a, b.
The common length , or measure, of these intervals is defined to be b − a
Theorem. Suppose that I is an interval with endpoints a, b and a < b, then I contains a rational number.
Proof. Define the length of I by ℓ := b−a. By the previous corollary , there
exists no ∈ IN such that
0 < 1/no < ℓ. Let A := {k| k an integer and k/no < a}. A is nonempty, since the
negative integers
are not bounded from below. Let ko belong to A. Set B := {k| k an integer and k
≥ ko}∩A. Also,
A is bounded from above by a · no, which shows that B is in fact a finite set of
integers. Let K be
the largest member of B and therefore of A, then K + 1
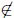 A. Let r := (K +
1)/no, then
A. Let r := (K +
1)/no, then
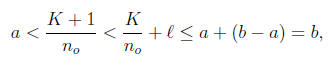
which shows that the rational r ∈ (a, b) ⊆ I.
Corollary. Each interval with nonzero length contains an infinite number of rationals.
Defn. A real number is said to be irrational if it is not rational.
Remark: Each interval with nonzero length contains an uncountably
infinite number of irrationals.
(Proved later.)
We establish a few other facts about irrational numbers and also prove
directly that each interval
of positive length contains an infinite number of irrationals.
Lemma. The product of a nonzero rational with an irrational is irrational.
Proof. Suppose that q1 · α = q2, where q1,
q2 are rational and α is irrational. Since q1 ≠ 0, then
α =q2/q1 and it follows that α is rational. Contradiction.
Lemma. If m is an odd integer, then m2 is odd.
Proof. If m is odd, then there exists an integer k such that m = 2k + 1. In this
case m^2 =
2(2k^2 + 2k) + 1.
Lemma. sqrt(2) is irrational.
Proof. Suppose that sqrt(2) = m/n where m, n are integers with n > 0. We may
assume that the
rational is in lowest terms (i.e. m and n have no common factors ). Squaring the
equation and
multiplying by n^2, we obtain that m^2 = 2n^2. This shows that m^2 is even. By
the lemma m must
be even and equivalently that it contains 2 as a factor. This shows 4k^2 = 2n^2
for some integer k.
Consequently, n is even and 2 appears as one of its
factors. Contradiction, since m/n was supposed
to be in lowest terms.
Theorem. Each interval with nonzero length contains
an infinite number of irrationals.
Proof. Let a, b be the endpoints of the interval I. Consider the interval
(a/sqrt(2), b/sqrt(2)). It has length
(b−a)/sqrt(2) > 0, and so contains a nonzero rational number q. It follows that
 is between a and
is between a and
b and hence belongs to I.
Defn. The absolute value of a real number a is defined by
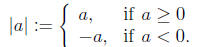
Lemma. The absolute value function has the following properties:
1. |a| ≥ 0 for all a ∈ IR.
2. ±a ≤ |a|
3. | − a| = |a|
4. |a · b| = |a| · |b|
5. Suppose α ≥ 0, then
|a| ≤ α if and only if −α ≤ a ≤ α.
6. |a + b| ≤ |a| + |b|
7. ||b| − |a|| ≤ |b − a|
Proof. To prove property 1, ‘case it out.’ Either a ≥ 0 or
a < 0. In the first case |a| = a ≥ 0. In
the second case, |a| = −a > 0, since a < 0. Property 2 follows similarly.
Properties 3 and 4 are left
for the student.
To prove property 5, notice that |a| ≤ α is equivalent to
the statement ±a ≤ α. Using the elementary
order properties, it is easy to see that this last statement is equivalent to
both inequalities :
a ≤ α and −α ≤ a. This is equivalent to the statement on the right hand side of
property 5.
To prove property 6, set α = |a| + |b| and apply property 5 after verifying that
±(a + b) ≤ α.
To prove property 7, use the fact that |b| = |(b − a) + a| ≤ |b − a| + |a| and
subtract |a| from each side. This shows that |b| − |a| ≤ |b − a|. By symmetry in
a and b, one proves that
|a| − |b| ≤ |a − b| = |b − a|.
| Prev | Next |