MATH 403: Homework 12 Solutions
1. There are several ways to do some of these, so these are just examples.
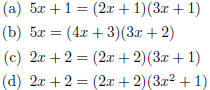
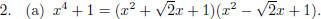
Note: This is not obvious but not hard to attack. Since there are no roots in R
there
are no linear factors in R[x] and so it must factor into two quadratics both in
R[x]. We
don't know that it factors into something like (x2+ax+1)(x2+bx+1) but this is a
good
first start since any other options would have leading or constant coefficients
which were
not integers and that would be awful so we give this a shot.
Expanding the right gives us x4 + 1 = x4 + (a + b)x3 + (ab + 2)x2 + (a + b)x + 1
and
equating coefficients gives us a + b = 0 and ab = -2. Solving this gives us our
result and
we're darned lucky it worked, too!
(b) We know that x + 6 (aka x - 1) is a factor since x = -6 (aka x = 1) is a
root . Long
division gives us the other, x2 + x + 1, and so x3 + 6 = (x + 6)(x2 + x + 1).
Note: x = 2 and x = 4 are also roots.
3. (a) x5 + 9x4 + 12x2 + 6: Eisenstein's Criterion with p = 3 does the job.
(b) x3-3x+3: If f(x) = x3-3x+2 then reduction mod p
= 2 yields 
= x3+x+1 ∈
Z2[x].
Since this is degree 3 it's irreducible over Z2 iff it has no roots and testing
x = 0, 1 tells
us it doesn't. The Mod-p Test then tells us that f(x) is irreducible over Q.
Note: Eisenstein works here too, with p = 3.
(c) In 2(a) we showed that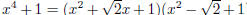 
in R[x]. Now then
suppose
x4 + 1 factored over Q. Since it has no linear factors (because no rational
roots) it must
factor into two quadratics in Q[x]. But these two quadratics are then also in
R[x] and
then we have two different factorizations over R which contradicts the fact that
R[x] is a
UFD.
Note: These factorizations are " different " in the sense that they're not just
rearranged or
replaced by associates in R[x] since the associates are obtained by multiplying
by nonzero
real numbers (units).
(d) x3 + 2x2 + 4x + 1: If f(x) = x3 + 2x2 + 4x + 1 then reduction mod p = 3
yields
= x3 +2x2 +x+1 ∈ Z3[x]. Since this is degree 3 it's irreducible over Z3
iff it has no
roots and testing x = 0, 1, 2 tells us it doesn't. The Mod-p Test then tells us
that f(x) is
irreducible over Q. Note that p = 2 does not work here.
(e) x3 +3x2 +2. If f(x) = x3 +3x2 +2 then reduction mod p = 5 yields = x3
+3x2 +2.
Since this is degree 3 it's irreducible over Z5 iff it has no roots and testing
x = 0, 1, 2, 3, 4
tells us it doesn't. The Mod-p Test then tells us that f(x) is irreducible over
Q. Note
that p = 2, 3 do not work here.
(f) x5+5x2+1: If f(x) = x5+5x2+1 then reduction mod p = 2 yields =
x5+x2+1 ∈
Z2[x]. No roots in Z2 tells us there are no linear terms but this may
factor into a degree
2 term and a degree 3 term. Let's check all possible degree 2 terms which don't
factor
themselves. There is only x2+x+1 long division shows us that does not factor
into .
Therefore is irreducible over Z2 and the Mod-p Test then tells us that
f(x) is
irreducible over Q.
4. Observe that there are p2 polynomials of the form x2 +
ax + b in Zp since there are p choices
for each of a and b.
Now then, a polynomial which is reducible over Zp may be rewritten in
the form (x-c)(x-d),
where c and d are the roots. So how many of these are there? Well, there are p
choices if c = d
and if c ≠ d then there are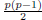 
choices; the division by 2 eliminates repeated pairs.
Therefore there are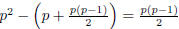 
polynomials irreducible over Zp.
5. Look at x4 +x3 +x2 +1 ∈ Z3[x]. This polynomial has no linear terms since
there are no roots
(try x = 0, 1, 2.)
But maybe it has two irreducible quadratic factors ? In Z3[x] there are only
three irreducible
quadratic polynomials with leading coefficient 1. Note that we can ignore those
with leading
coefficient 2 since if 2x2 + ... is a factor then so is 2(2x2 + ...) = x2 + ....
These three polynomials are x2 + 1, x2 + x + 2 and x2 + 2x + 2 (discovered by
brute force) so
we divide our polynomial by each of these in turn and we find a remainder each
time.
Therefore the quotient ring Z3[x]/ <
x4 + x3 + x2 + 1 > is a field. The elements in this field
have the form ax3 + bx2 + cx + d + <
x4 + x3 + x2 + 1 > since higher powers simplify via x4 +
<
x4 + x3 + x2 + 1 > = 2x3+2x2+2+
<
x4 + x3 + x2 + 1 >. Since a, b, c, d ∈ Z3 there are 3·3·3·3 =
81 possible elements.
6. Look at x3+x+1 ∈ Z2[x]. This polynomial is irreducible over Z2 by the 2,
3-test since there are
no roots. Therefore the quotient ring Z2[x]/ <
x3 + x + 1 > is a field. The elements in this field
have the form ax2+bx+c+<
x3 + x + 1 > since higher powers simplify via x3+<
x3 + x + 1 > =
-x - 1 + <
x3 + x + 1 > = x + 1 + <
x3 + x + 1 >. Since a, b, c ∈ Z2 there are 2 · 2 · 2 = 8 possible
elements.
7. We know from problem 4 that there are
polynomials of the form x2 + ax + b which are
irreducible over Zp. Pick any one, denote it x2 + a'x + b'. Then Zp[x]/
<
x2 + a'x + b' > is a
field of with elements of the form αx + β + <
x2 + a'x + b' > with α, β ∈ Zp. Since there are p
choices for each of α, β there are p2 elements.
| Prev | Next |