Applications of Number Theory
3.1. Representation of Integers.
Theorem 3.1.1. Given an integer b > 1, every positive integer n can be expresses
uniquely as
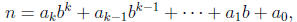
where 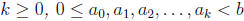 , and are all integers.
, and are all integers.
Definition 3.1.1. Base b expansion of n is
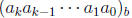 if the ai are as
if the ai are as
described in Theorem 3.1.1.
Example 3.1.1. Here are examples of common expansions other than the more
familiar decimal expansion .
• Binary expansion is the base 2 expansion.
• Octal expansion is the base 8 expansion.
• Hexadecimal expansion is base 16 expansion. The symbols A through
F
are used to represent 10 through 15 in the expansion.
Discussion
Theorem 3.1.1 asserts that each positive integer n can be expressed uniquely as
a linear combination of powers of a fixed integer b > 1. The coefficients in the
linear combination must be less than b and must be greater than or equal to
zero .
These coefficients are , by definition, the digits of the base b expansion
of n, n =
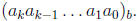
3.2. Constructing Base b Expansion of n. Use the division algorithm to
get
the base b expansion of n:
1. 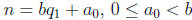 and
and 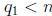 .
.
2. 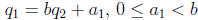 and
and 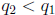 .
.
3. 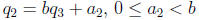 and
and 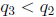 .
.
4. etc. until 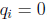 .
.
Then n = ![]() .
.
Example 3.2.1. Find the binary expansion of 42.
Solution : We can use the division algorithm to get the ai's
42 = 2(21) + 0
21 = 2(10) + 1
10 = 2(5) + 0
5 = 2(2) + 1
2 = 2(1) + 0
1 = 2(0) + 1
This gives us 42 = (1)(25) + (0)(24) + (1)(23) + (0)(22) + (1)(21) + 0. Thus the
binary expansion of 42 is (101010)2.
Example 3.2.2. Find the hexadecimal expansion of 42.
Solution : This time we use 16 for b.
42 = 16(2) + 10
2 = 16(0) + 2
So the hexadecimal expansion of 42 is (2A)16(recall we use A = 10 in
hexadecimal
notation).
Example 3.2.3. Find the decimal notation of the octal representation (1024)8.
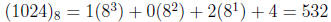
3.3. Cancellation in Congruences.
Theorem 3.3.1. Suppose GCD(c,m) = 1 and ac ≡ bc(mod m). Then a ≡
b(mod m).
Proof. Suppose GCD(c,m) = 1 and
ac ≡ bc(mod m). (We may assume m > 1 so that c ≠ 0.) Then
ac − bc = c(a − b) = km
for some integer k. This implies
c|km.
Since GCD(c,m) = 1, Lemma 2 from Module 5.2 asserts that if c|km, then
c|k.
Write k = cd for some integer d, and substitute for k in the equation above:
c(a − b) = km = (cd)m = c(dm).
Since the cancellation law holds for integers and c ≠ 0,
we can cancel c to get
a − b = dm.
Thus, a ≡ b(mod m).
Discussion
Theorem 3.3.1 provides a criterion for being able to cancel when you have a
congruence. Notice that in order to perform the cancellation, the modulus m and
the
factor to be cancelled must be relatively prime. Here is an example to
illustrate why.
Example 3.3.1. 3·6 ≡ 1· 6(mod 12), but 3 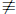 1(mod 12). The reason cancellation
1(mod 12). The reason cancellation
fails is that 6 and 12 are not relatively prime.
Example 3.3.2. 3 · 6 ≡8 · 6(mod 5). Here 6 and 5 are relatively prime and we
can easily check that 3 ≡ 8(mod 5).
3.4. Inverses mod m.
Definition 3.4.1. An integer a' is a (multiplicative) inverse to a modulo m
if
aa' ≡ 1(mod m).
Example 3.4.1. The inverse of 14 modulo 9 is 2, since 14 · 2 ≡28 ≡1(mod 9).
There is no inverse to 6 modulo 9, however.
In general, an “inverse” refers to something that “undoes” another thing leaving
something that is an “identity”.
• With regular multiplication of real numbers, the inverse of x is
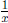 since
since 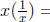
1. Inverses do not necessarily exist if we look only at integers.
• With regular addition of real numbers, the inverse of x is −x since x+(−x) =
0,
• With matrices and matrix multiplication, the inverse of a matrix, A, is a
matrix A-1, such that AA-1 = A-1A = I, where I is the identity matrix.
Not all matrices have inverses.
• With functions and composition, the inverse of a function, f, is a function,
f -1, such that (f o f -1)(x) = ( f -1 o f)(x) = x = identity(x). Not all
functions have inverses.
• Not all integers, even nonzero integers, have inverses modulo m. Moreover,
if an inverse does exist it is not unique. This last part is different from all
the
other ones mentioned before! We shall see below, however, that if an integer
a has an inverse modulo m, then it has a unique inverse lying between 0 and
m.
| Prev | Next |