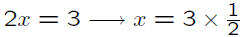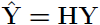Matrix Approach to Simple Linear Regression
Use of Inverse
• Inverse similar to using reciprocal of a scalar
• Pertains to a set of equations
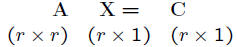
• Assuming A has an inverse:
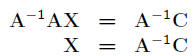
Random Vectors and Matrices
• Contain elements that are random variables
• Can compute expectation and (co)variance
• In regression set up,
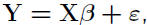both ε and Y are random
vectors
• Expectation vector:
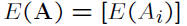
• Covariance matrix: symmetric
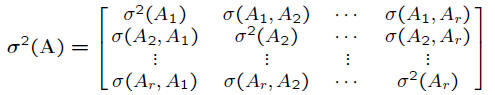
Basic Theorems
• Consider random vector Y
• Consider constant matrix A
• Suppose W = AY
– W is also a random vector
– E(W) = AE(Y)
– 
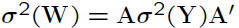
Regression Matrices
• Can express observations
Y = Xβ +ε
• Both Y and ε are random vectors
E(Y)
= Xβ+E(ε)
= Xβ
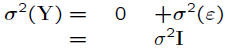
• Express quantity Q
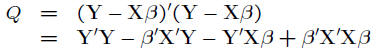
• Taking derivative →
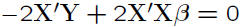
• This means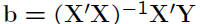 
• The fitted values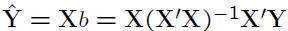 
• Matrix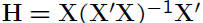 
is called the hat matrix
– H is symmetric, i.e., H' = H
– H is idempotent, i.e., HH = H
• Matrix H used in diagnostics (chapter 9)
Residuals
• Residual matrix
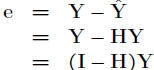
• e a random vector
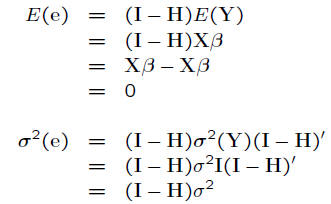
ANOVA
• Quadratic form defined as
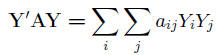
where A is symmetric n × n matrix
• Sums of squares can be shown to be quadratic forms (page
207)
• Quadratic forms play significant role in the theory of linear
models when errors are normally distributed
Inference
• Vector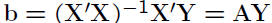 
• The mean and variance are
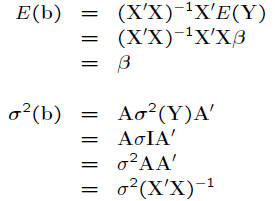
• Thus, b is multivariate Normal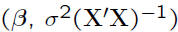
• Consider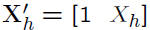 
• Mean response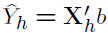 
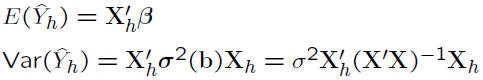
• Prediction of new observation
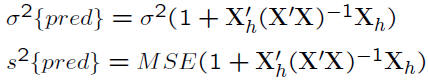
Chapter Review
• Review of Matrices
• Regression Model in Matrix Form
| Prev | Next |