MCE Training of MQDF-based Classifiers
Abstract
In this study, we propose a novel optimization algorithm
for minimum classification error (MCE) training
of modified quadratic discriminant function (MQDF)
models. An ellipsoid constrained quadratic programming
(ECQP) problem is formulated with an efficient
line search solution derived, and a subspace combination
condition is proposed to simplify the problem in
certain cases. We show that under the perspective of
constrained optimization, the MCE training of MQDF
models can be solved by ECQP with some reasonable
approximation, and the hurdle of incomplete covariances
can be handled by subspace combination. Experimental
results on the Nakayosi/Kuchibue online handwritten
Kanji character recognition task show that compared
with the conventional generalized probabilistic
descent (GPD) algorithm, the new approach achieves
about 7% relative error rate reduction.
1. Introduction
For handwritten character recognition, modified
quadratic discriminant function (MQDF) [4] based classifiers
achieve quite good performance. Beyond maximum
likelihood (ML) training, minimum classification
error (MCE) [3] training can effectively improve the
recognition accuracy [5]. However, MCE training is
a more difficult optimization problem. Conventionally,
the generalized probabilistic descent (GPD) approach,
which only utilizes the first order derivatives, works decently
for MQDF models [5]. However, it is critical to
fine tune the learning rate to achieve better accuracy.
In this study, motivated by the progress in optimization
area, we address the problem using novel optimization
algorithms for MCE training on MQDF mod-
*This work has been done when the first author was an intern at
Microsoft Research Asia, Beijing, China.
els, which should be able to effectively utilize more
information than gradient. Intuitively, second order
approximation leads to a quadratic optimization problem,
which is a good starting point beyond gradient
based approaches. As the theory of convex optimization
and interior point matures [2], a general quadratically
constrained quadratic programming (QCQP) [8]
problem can be solved by the strategy of relaxation
- convex optimization. In this study, we show that
the nature of MCE criterion applied on MQDF models
leads to a special case of QCQP, namely ellipsoid
constrained quadratic programming (ECQP), which can
be efficiently solved without relaxation. Furthermore,
we derive a subspace combination condition to simplify
the problem in certain cases. Based on the constrained
optimization perspective of discriminative training, the
optimization problem of MCE on MQDF models can
be represented as an ECQP under a popular approximation,
and the subspace combination condition is useful
to deal with partially recorded covariances.
To verify the effectiveness of the proposed approach,
we conducted experiments on the Nakayosi/Kuchibue
online handwritten Kanji character recognition
databases. Results show that the new optimization
algorithm outperforms GPD-based MCE training in
terms of character recognition accuracy.
2. Ellipsoid Constrained Quadratic Programming
2.1 ECQP Definition and Solution
To effectively utilize second order information in optimization,
we intuitively pay our attention to the general
QCQP problem. In general, such a problem can
be solved by the strategy of relaxation - convex optimization.
However, we observe that in MCE training,
the trust region according to any reasonable step size
control should be convex, which leads to an ellipsoid
constraint when represented in a second order form.
Accordingly, we introduce the following special case
termed as ellipsoid constrained quadratic programming
(ECQP) here:
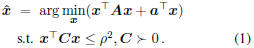
We will show that the problem can be efficiently solved
without relaxation by the algorithm introduced below,
which makes it more feasible for many real problems.
Without loss of generality, we further assume that
both A and C are symmetric. By applying Lagrange
multipliers method, the corresponding objective function
of the dual problem is:
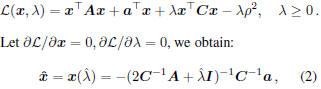
where 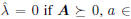 the row space of A, and
the row space of A, and
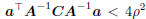 ; otherwise it is the value satisfying
; otherwise it is the value satisfying
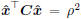 . The solution can be efficiently
. The solution can be efficiently
conducted by a line search, and a detailed implementation
based on the Newton’s method is shown below:
Table 1. A Newton’s approach to ECQP
| Let m be the minimum eigenvalue of C-1A If 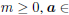 span(A) and span(A) and
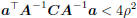 return 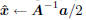 Else λ <- max(-m, 0)+ a positive minor value if 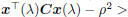 tolerance tolerance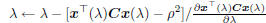 return 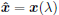 |
2.2 Subspace Combination Condition
When finding 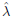 by the algorithm in Table 1, we
by the algorithm in Table 1, we
should compare the corresponding 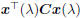 with
with
ρ2 at each step, and the computational cost is proportional
to the dimension of x. We show that in some
cases, a part of 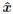 is guaranteed to be along a certain
is guaranteed to be along a certain
direction in the corresponding subspace, which can be
used to reduce the problem dimension.
Suppose A and C can be decomposed to two parts,
and one part of A is in proportional to the corresponding
one in C, or equivalently:
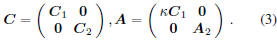
Accordingly, we can decompose
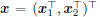 and
and
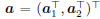 . Let
. Let 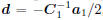 , we can prove
, we can prove
that the original problem is equivalent to the following
one:
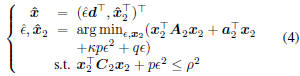
where 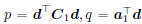 . Obviously, p
≥ 0, and
. Obviously, p
≥ 0, and
the new problem is also an ECQP problem that can be
solved by the algorithm in Table 1. Now the subspace
related to x1 is combined to one parameter ², and the
relations of Eq.(3) is termed as the subspace combination
condition for ECQP, whose physical meaning can
be clarified as: if the contours of constraint and objective
function are similar in a subspace, the final solution
in this subspace is guaranteed to be on the direction towards
the critical point of the objective function in the
subspace.
3. ECQP Solution for MCE Training of
MQDF Parameters
In this section, we show that with a widely adopted
approximation in discriminative training, the optimization
with respect to mean vector in MQDFs for MCE
criterion can be converted into an ECQP problem.
3.1. MQDF-based Classifiers
Denoting
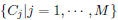 as a set of M character
as a set of M character
classes, we can model each of them by a Gaussian
distribution with mean μj and covariance Σj in a Ddimensional
feature space. By setting the (K + 1)th to
Dth eigenvalues of Σj as a class-dependent constant δj ,
a modified quadratic discriminant function (MQDF) is
proposed. Given a feature vector x, its probability density
function (pdf) of jth class can be calculated as[4]:
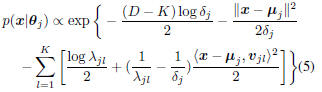
where θj represents the parameters of the MQDF
model of Cj , namely: μj , the mean vector of class
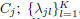 , the first K leading eigenvalues of Σj ;
, the first K leading eigenvalues of Σj ;
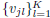 , the corresponding eigenvectors; δj , the class
, the corresponding eigenvectors; δj , the class
dependent constant. In practice, setting δj as the average
of (K+1)th toDth eigenvalues works well [4]. Note
that in MQDF model, only the first K leading eigenvalues
and eigenvectors need be recorded.
3.2. MCE Training of MQDFs by ECQP
Given a training set 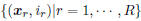 , where
, where
xr and ir are the feature vector and the label index of
the rth training sample, respectively, the MCE criterion
applied to MQDF models can be formulated as [9]:
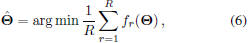
where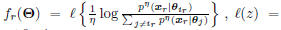
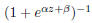 is the sigmoid smoothing function, and
is the sigmoid smoothing function, and
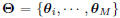 is the whole model parameter set.
is the whole model parameter set.
The objective function (6) is highly nonlinear and often
involves millions of parameters to optimize. In practice,
a sequential gradient descent algorithm (a.k.a, GPD algorithm),
is used to optimize Θ with the following parameter
updating formula:
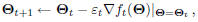
where index “t” represents the cumulative training samples
presented so far (in random order).
Practically, it is somewhat cumbersome to adopt this
strategy because: (i) the use of gradient makes the algorithm
converge very slowly and easily trapped by poor
local optimums; (ii) the learning rate εt is very critical,
but there is no theoretically sound method to determine
it. A popular scheme is:
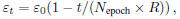
where Nepoch is the number of epoch to be performed
(one pass of all training samples is called one epoch).
Instead of fine tuning εo to constrain each step size,
we impose a statistically sound Kullback-Leibler divergence
(KLD) based locality constraint, which is practically
useful [6], then find the optimal point within the
corresponding trust region, i.e.,
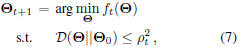
where Θo is the current parameters of seed models, i.e.,
Θt in tth update, and D represents KLD between two
statistical models. In the rest of this section, we will
show how it can be transformed into an ECQP problem.
Only mean update will be considered in this study.
Given a training sample (xt, it), the gradient of ft
w.r.t θj can be calculated as:
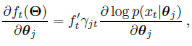
where 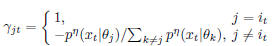 .
.
Here we adopted the assumption that 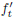 and γjt keep
and γjt keep
constant in each iteration, which has been widely used
and verified [9, 6]. Accordingly, we obtain the following
second order derivatives:
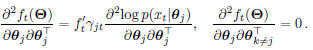
By substituting the Gaussian distributions for
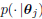
and only considering mean update, the Hessian of
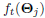 is constant everywhere, thus the objective function
is constant everywhere, thus the objective function
is a quadratic function. With this observation, we
come up with the following ECQP problem with respect
to means:
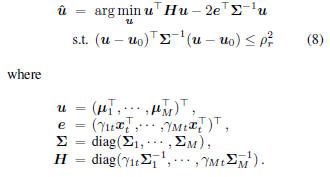
A hurdle to this problem is that the covariances
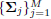 are only partially recorded. However, we observe
are only partially recorded. However, we observe
that in any subspace corresponding to the mean
of a model j, the combination condition introduced in
section 2.2 holds. Consequently, we can combine each
subspace to a scalar space and come up with the following
equivalent ECQP problem:
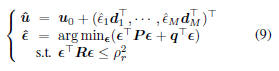
where 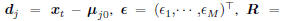
diag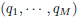 , P = diag
, P = diag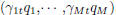 , q =
, q =
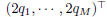 , and
, and 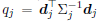 . By the same
. By the same
trick in Eq.(5), qj can be calculated as:
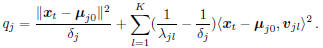
In practice, to make training stable and focus on those
problematic samples, ρt is set as follows:
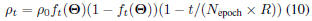
4. Experiments
To evaluate the proposed algorithm, we conduct experiments
on an online handwritten character recognition
task using the Nakayosi/Kuchibue Japanese character
databases[7] with a vocabulary of 2965 level-1 Kanji
characters in JIS standard. The Nakayosi database consists
of about 1.7 million character samples from 163
writers, and the Kuchibue database contains about 1.4
million character samples from 120 writers. We randomly
select about 92% samples from the Nakayosi
database to form the training data set, 75% samples
from the Kuchibue database to form the testing data set,
while the remaining samples from both databases are
used to form a development set for tuning control parameters.
As for feature extraction, a 512-dimensional raw feature
vector is first extracted from each handwriting sample
by using the procedure described in [1]. Then we
apply LDA to reduce the feature dimension to 192.
In our MQDF models, K was set to 4. In MCE
training, the control parameters of η, α, β was set to
be 0.2, 0.022 and 0, respectively. When using sequential
gradient descent, the initial learning rate ε0 was fine
tuned to be 0.05, while in the ECQP training, the control
parameter 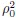
was set to 0.01 and decreased to zero
( as specified in Eq. (10) ) to make training more stable
and converge. Both control parameters are fine tuned
for the best performances. To speed up the training process,
we use the N-best list as the hypotheses space
instead of the whole character set, where N is set as
100 for both sequential gradient descent and ECQP algorithm.
The final comparison result is shown in Fig.
1, where “GPD” stands for sequential gradient descent
algorithm; “ECQP” stands for our proposed algorithm.
Using ECQP optimization, the error rate decreases from
1.97% to 1.52%, which achieves 22.8% error reduction,
a relative 7% error rate reduction compared with GPD.
5. Conclusion
In this paper, we propose an ECQP approach to performing
MCE training. An efficient solution of ECQP
without relaxation is first derived, and a subspace combination
condition is then discussed. Under the perspective
of constrained optimization, we show that MCE
training on MQDF models can be solved more effectively
by ECQP than conventional sequential gradient
descent algorithm. Effectiveness of our algorithm was
verified by experimental results on Nakayosi/Kuchibue
Japanese character database.
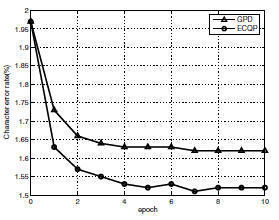
Figure 1. Comparison of character recognition
error rates of different algorithms on
Nakayosi/Kuchibue database.
References
[1] Z.-L. Bai and Q. Huo, “A study on the use of 8-directional
features for online handwritten Chinese character recognition,”
Proc. ICDAR-2005, pp.262-266.
[2] S. Boyd, L. Vandenberghe, Convex Optimization, Cambridge
University Press, 2004.
[3] B.-H. Juang, W. Chou and C.-H. Lee, “Minimum classification
error rate methods for speech recognition,” IEEE
Trans. Speech Audio Process., vol.5, no.3, pp.257-265,
May 1997.
[4] F. Kimura, K. Takashina, S. Tsuruoka, and Y. Miyake,
“Modified quadratic discriminant functions and the application
to Chinese character recognition,” IEEE Trans.
on PAMI, vol. 9, no. 1, pp.149-153, 1987.
[5] C.-L. Liu, H. Sako, and H. Fujisawa, “Discriminative
learning quadratic discriminant function for handwriting
recognition,” IEEE Trans. on Neural Networks, vol. 15,
no. 2, pp.430-444, 2004.
[6] P. Liu, C. Liu, H. Jiang, F.K. Soong, R.-H Wang, “A constrained
line search optimization method for discriminative
training of HMMs,” IEEE Trans. on ASLP, vol. 16,
no. 5, pp. 900-909. 2008.
[7] M. Nakagawa and K. Matsumoto, “Collection of online
handwritten Japanese character pattern databases and
their analysis,” International Journal on Document Analysis
and Recognition, vol. 7, pp.69-81, 2004.
[8] E. Phan-huy-Hao, “Quadratically constrained quadratic
programming: some applications and a method for solution”,
Ieischrift fur Operations Research , pp. 105-119
vo1 26, 1982.
[9] R. Schluter, Investigations on discriminative training criteria,
Ph.D. thesis, Aachen University, 2000.
| Prev | Next |