Nonlinear Programming Final Exam
section A
Indicate whether each statement is true (+) or false (o).
If false, briefly state why or give a
counterexample.
_____ 1. A barrier function adds a penalty to the
objective when the solution approaches a
boundary of the feasible region.
_____ 2. The number of "dependent" variables of the GRG
algorithm is equal to the number of
equality constraints.
_____ 3. The cubic interpolation procedure for
one-dimensional minimization requires the
computation of second derivatives.
_____ 4. The function xa is convex for x>0.
_____ 5. The feasible directions algorithm computes a search direction by solving an LP .
_____ 6. The Fibonacci method for one -dimensional
minimization requires the computation of
derivatives.
_____ 7. If all posynomials in a (posynomial) GP problem
are condensed into single terms,
then it is always possible to rewrite the resulting problem as an LP problem.
_____ 8. A linear function is neither convex nor concave.
_____ 9. The Gradient Projection method always follows the
boundary of the feasible region,
and never enters the interior.
_____ 10. The logarithm of the dual GP objective v(δ,λ) above is a concave function of δ and λ.
_____ 11. The logarithm of the dual GP objective v(δ,λ)
above is not a concave function of
both δ and λ, but becomes so if you eliminate
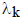 using
using
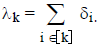
_____ 12. A locally optimal solution for a signomial
geometric programming problem must be
globally optimal.
_____ 13. The dual ("pseudo-dual") of a signomial GP
problem may have multiple local
maxima, but its global maximum will have the same objective value as the global
minimum of the primal signomial GP.
_____ 14. Penalty functions may be used for both equality
and inequality constraints , but barrier
functions may be used only for inequality constraints.
_____ 16. If the Lagrangian function L(x,λ) has a saddlepoint
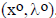 , then
there is zero duality
, then
there is zero duality
gap between primal and dual optimal solutions.
_____ 17. Consider the problem: min f(x) subject to gi(x)
≤ 0, i=1,2...m, x ≥ 0
(where gi satisfy
some constraint qualification) and its Lagrangian function
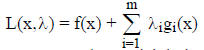
Then if f and gi are convex, the partial derivative of L with respect to each xj
must be
zero at the optimum.
_____ 18. For the problem in the previous statement ,
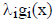 must be zero at the
optimum.
must be zero at the
optimum.
_____ 19. For the problem in the previous statement, either xj or
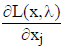 (or possibly both)
(or possibly both)
must be zero at the optimum.
_____20. The limit, as w → 0, of the function (c/w)w is ∞.
_____21.
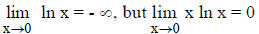
_____22. If we define the function
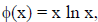 then
then
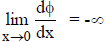
_____23. When the dual problem is solved, the primal variables of a posynomial
GP problem
are often computed by exponentiating the Lagrange multipliers of the
orthogonality
constraints.
_____24. The function f(x,y) = xy is a concave function of x and y.
_____25. If an algorithm is applied to a minimization problem with optimal value
zero, and the
objective value is approximately halved at each iteration, then we would say
that the
algorithm has a linear rate of convergence.
_____26. The Hessian matrix of (xtQx + cx) is 2Q.
_____27. In the QC/LD problem, the objective function is assumed to be quadratic.
_____28. If fi(x) is linear for i=1,2,...n, then the function F(x) defined by
F(x)= max{fi(x):
i=1,2,...n} is a convex function.
_____29. If a posynomial GP objective function continues to decrease as xj
→ 0
for some primal
variable xj, then the dual problem objective is unbounded.
_____30. If a posynomial GP objective function continues to decrease as xj
→ +∞
for some
primal variable xj, then the dual problem is infeasible.
_____ 31. Every posynomial function is convex.
_____ 32. The dual of a constrained posynomial GP problem has only linear
equality and
nonnegativity constraints.
_____ 33. If a primal GP constraint is slack, then all the weights of the terms
in that constraint
must be zero.
_____ 34. In the QC/LD problem, the variables are restricted to be integer-valued.
_____ 35. The gradient of the function f(x) = (xtQx + cx) is Qx + c.
_____ 36. Solving the QC/LD problem requires a one-dimensional search at each iteration.
_____ 37. The posynomial constraint gi(x) ≤1 has a convex feasible region.
_____ 38. It is always possible (e.g., by a change of variable ) to reformulate a
posynomial GP
problem so as to have a convex objective and convex feasible region.
_____ 39. The objective of the posynomial GP problem, i.e.,
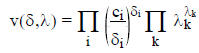
is a concave function of δ and λ.
_____ 40. In the "Golden Section Search" method, more than one-third of the
interval of
uncertainty is eliminated at each iteration (assuming that no function values
are equal).
_____ 41. If all posynomials in a (posynomial) GP problem are condensed into
single terms,
then the resulting problem has a feasible region which includes the original
feasible
region.
_____ 42. The Hessian matrix of a quadratic function is constant.
_____ 43. In Wolfe's complementary pivoting algorithm for QP, if a single
artificial variable is
used, then the tableau does not require an objective row.
_____ 44. The gradient projection method computes Lagrange multipliers at each
iteration, and
stops when they have the appropriate sign.
_____ 45. "Quasi-Newton" search methods for unconstrained minimization require
the
computation of second partial derivatives.
_____ 46. Newton's method for unconstrained minimization requires the
computation of second
partial derivatives.
_____ 47. If you guess at the value of some primal GP variable and then fix it
at this value, the
dual GP problem becomes more difficult to solve.
_____ 48. In a "generalized linear programming" problem, the column of
coefficients of the
variables must be selected as well as the variables.
_____ 49. The function eax is convex only for a ≥ 0.
_____ 50. The Davidon-Fletcher-Powell (DFP) algorithm requires the computation
of partial
derivatives.
_____ 51 . If a posynomial function is "condensed" into a monomial, the monomial
function (if
not equal) is an overestimate of the posynomial function.
_____ 52 . Wolfe's method for quadratic programming requires a one-dimensional
search at
every iteration.
_____ 53. If a constrained nonlinear programming problem satisfies a "constraint
qualification",
then a point which satisfies the Karush-Kuhn-Tucker conditions must be an
optimal
solution.
_____ 54. A barrier function allows a constraint to be violated, but adds a
penalty if the
constraint is violated.
_____ 55. The GRG algorithm requires the use of a one-dimensional search method.
_____ 56. The Feasible Directions algorithm requires the use of a
one-dimensional search
method.
_____ 57. If a constrained nonlinear programming problem satisfies a "constraint
qualification",
then the Karush-Kuhn-Tucker conditions must be satisfied by an optimal solution.
_____ 58. The function eax is convex for all values of a.
_____ 59. In Wolfe's complementary pivoting method for quadratic programming,
the
complementary slackness conditions are satisfied after each iteration.
_____ 60 . The tableau for Wolfe's method for quadratic programming includes
columns for
both primal and dual variables.
_____ 61. The function xa is convex for a ≥ 0.
_____ 62. If a nonlinear programming problem has only linear constraints, then
any point which
satisfies the Karush-Kuhn-Tucker conditions must be optimal.
_____ 63. The Fletcher-Reeves method is also known as a "Quasi-Newton" method.
_____ 64. The quadratic interpolation procedure for one-dimensional minimization
requires the
computation of derivatives.
_____ 65. If the GRG algorithm were applied to a LP problem, it would produce,
at each
iteration, the same solution as the simplex algorithm for LP.
_____ 66. A penalty function allows a constraint to be violated, but adds a
penalty if the
constraint is violated.
_____ 67. The Lagrangian dual of a convex quadratic programming problem is a
quadratic
programming problem with only nonnegativity constraints on the dual variables.
_____ 68. Powell's algorithm for unconstrained minimization requires the
computation of partial
derivatives.
_____ 69. The Davidon-Fletcher-Powell method is also known as the "Conjugate
Gradient"
method.
_____ 70. In the QC/LD problem, the objective function is assumed to be convex.
| Prev | Next |