p-adic Number
Theorem: If one has a solution of the form
x2 = b mod p,
with p > 2, then the solutions obtained when raising p to higher powers exist,
and will form a coherent sequence.
Proof: The proof will be by induction. The hypothesis of the theorem takes
care of the first part of the induction. Now assume we have
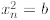mod pn,
so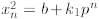 
for some
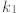. We want to know if there exists a
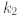such that
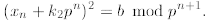
Expanding and replacing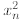 
with
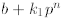we get
Cancelling out the b's and the term divisible by
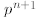we
get
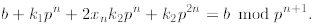
Now, dividing by p n we get
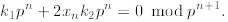
We will now show that no matter what 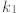is, we can choose
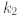so that
the equality is true. Assume 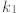= 2m (i.e., is even). Then let
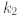= (p -
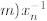mod p. Assume 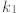= 2m + 1, then let 
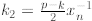. Of
course,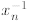 
will exist because p is a prime. Therefore we will be able
to carry on the
sequence infinitely.
Even with just our one solution of x 2 = 2 (the 7-adic solution), we
have shown that there is at least one element in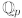 
which is not in Q, and
therefore 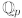is strictly bigger than Q.
In what will at first seem to take us in a new direction, we define the
p-adic valuation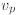 
on the rational numbers .
Definition The p-adic valuation of a non-zero integer n is the unique number
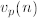such that
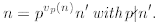
We extend this definition to a rational number
by saying
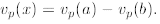
Finally, we define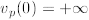 
.
Now we define the p-adic absolute value.
Definition For any x ∈ Q not equal to 0, we define the p-adic absolute value
of x to be
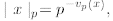
and if x = 0, we set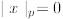 
.
We refer to that as an absolute value, but to ensure that it is an absolute
value we must verify the following three properties (which, if true, will show
that this absolute value is a non -archimedian absolute value.)
1. l xl = 0 if and only if x = 0.
2.
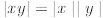for all x, y ∈ Q.
3.
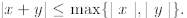
To show this is true, we will rely on the following Lemma:
Lemma For all x and y ∈ Q, we have
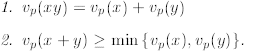
Proof: We begin by assuming that both x and y are
integers. Let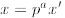 
and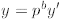 
, with both x' and y' not divisible by p . Now
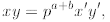
and therefore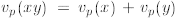 
. To prove the second
part of the
Lemma, we assume that a ≤ b. (We can always reverse the roles of x and y
if we need to.) With this in mind,
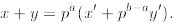
Therefore,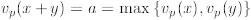 
: Now we must
make sure this
is also true when x is not an integer but a rational number . Assume
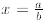
and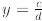 
, then:
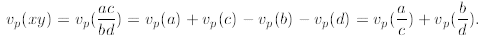
And,
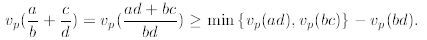
Now, assume that the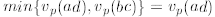 
. Then,
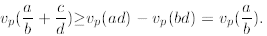
This concludes the proof of the Lemma.
We are now ready to show that the p-adic absolute value as we defined
it is, in fact, an absolute value and, more specifically, is a non-archimedian
absolute value.
Theorem: Our definition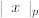 
above defines a non-archimedian absolute
value on Q.
Proof:
1. For the first property , note that the absolute value cannot equal zero
for any finite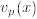 
. Therefore
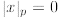if and only if x = 0.
2. We can prove the second property simply by using the Lemma and
manipulating the definitions.
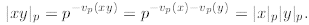
3. Once again, we can prove this property directly from the Lemma.
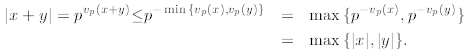
This concluces the proof.
With more time it could be shown that the p-adic numbers dealt with in
the first half of the paper are a completion of Q with respect to the p-adic
absolute value dealt with in the second half of the paper.
Acknowledgements: I would like to thank Harvey Keynes for telling me
about this program, the University of Minnesota for paying me to attend
lectures and read math texts , and most of all Professor Paul Garrett for
giving me the opportunity to work here this summer and for his daily lectures
and assistance.
Created using
.
| Prev | Next |