The Generalized Routh-Hurwitz Criteria for Quadratic and Cubic Polynomials
The Generalized Routh-Hurwitz Criteria for Quadratic and Cubic Polynomials
Quadratic polynomials
Consider the polynomial
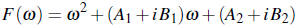
with
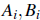 real.
real.
Phase velocity direction
The number of roots of F (w) = 0 with positive real part is given by the number
of sign changes
in the sequence
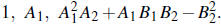
The number of roots of F (w)=0 with negative real part is
given by the number of sign changes
in the sequence
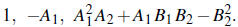
Phase velocity direction: real coefficients
If all the coefficients in the polynomial are real (i.e., if B1 = B2 = 0), then
we get the following
result:
If A1 > 0 and A2 > 0 then both roots have negative real part.
If A1 > 0 and A2 < 0 then one root has positive real part and one root has
negative real part.
If A1 < 0 and A2 > 0 then both roots have positive real part.
If A1< 0 and A2 < 0 then one root has positive real part and one root has
negative real part.
Instability
The number of unstable roots of F(w) (i.e., the number with positive imaginary
part) is given
by the number of sign changes in the sequence
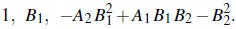
The number of stable roots of F(w) (i.e., the number with
negative imaginary part) is given by
the number of sign changes in the sequence
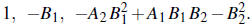
Cubic polynomials
Consider the polynomial
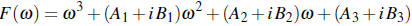
with
![]() real.
real.
Phase velocity direction
The number of roots of F(w) = 0 with positive real part is given by the number
of sign changes
in the sequence
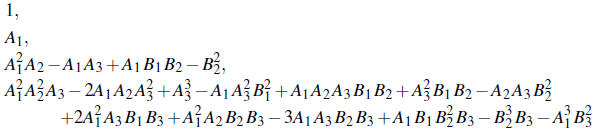
The number of roots of F(w)=0 with negative real part is
given by the number of sign changes
in the sequence
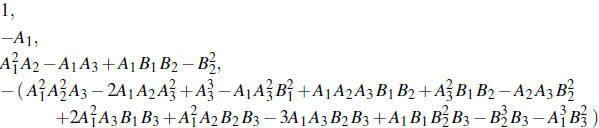
Instability
The number of unstable roots of F(w) (i.e., the number with positive imaginary
part) is given
by the number of sign changes in the sequence
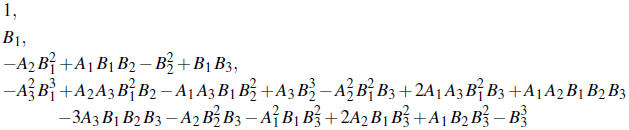
The number of stable roots of F(w) (i.e., the number with
negative imaginary part) is given by
the number of sign changes in the sequence
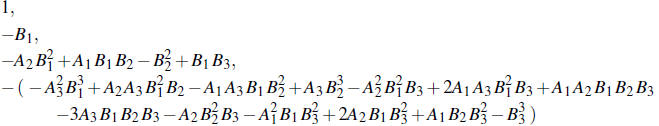
| Prev | Next |