Factoring Polynomials
A polynomial is a sum or subtraction of monomials . i.e.
10x2 +15x is a polynomial and
so is x3 + 3x2 − 5x + 9 .
In any factorization problem, the first thing to look at is the greatest common
factor.
Factoring out the Greatest Common Factor (GCF)
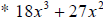
In this polynomial, 9 is the greatest integer that divides 18 and 27 and x2 is
the greatest
expression that divides x3 and x2.
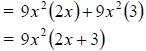
Some polynomials may have a GCF of 1, but appropriate grouping may lead to
possible
factorization.
Factoring by Grouping
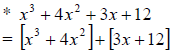
Common factor in x3 + 4x2 is x2 and common factor in 3x+ 12 is 3. These can be
factored
as:
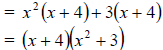
Factoring Trinomials
A strategy for factoring ax2 + bx + c,
1. Find 2 numbers whose product is ac and whose sum gives b. Say these numbers
are u
and v.
2. Re-write the trinomial such as ax2 + ux+ vx + c
3. Use factoring by grouping to find the factors
Here is an example:
* x2 + 3x −18
We need to find two numbers such that their product is -18 and their sum is 3.
Let’s find
the factors of -18
| Factors of -18 |
18, -1 | -18, 1 | 9, -2 | -9, 2 | 6, -3 | -6,3 |
| Sum of factors |
17 | -17 | 7 | -7 | 3 | -3 |
Our desired numbers are 6 and -3.
We will now re-write our trinomial : x2 + 6x − 3x −18
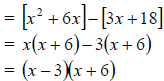
Let’s look at another example whose leading coefficient is not 1:
* 8x2 −10x − 3
We need to find two numbers such that their product is -24 and their sum is -10.
Let’s
find the factors of -24.
| Factors of -24 |
24, -1 | -24, 1 | 12, -2 | -12, 2 | 8,-3 | -8,3 | 6, -4 | -6, 4 |
| Sum of factors |
23 | -23 | 10 | -10 | 5 | -5 | 2 | -2 |
Our desired numbers are -12 and 2.
We will now re-write our trinomial : 8x2 −12x + 2x − 3
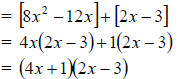
| A Strategy for Factoring a Polynomial 1. If there is a common factor, factor out the GCF. 2. Determine the number of terms in the polynomial and try factoring as follows a. If there are two terms, then can the binomial be factored by any of the special forms? i.e. Difference of two squares a2 - b2 = (a+ b)(a-b) Sum of two cubes a 3 + b3 = (a+ b) (a2 - ab + b2) Difference of two cubes a3 - b3 = (a- b) (a2 + ab + b2) b. If there are three terms, then is the trinomial a perfect square trinomial? i.e. a2 +2ab + b2= (a+ b)2 and a2 - 2ab + b2= (a- b)2 If not, try the method shown earlier for factorization of trinomials c. If there are four or more terms, try factoring by grouping. 3. Check to see if any factors with more than one term in the factored polynomial can be factored further. If so, factor completely. |
Let’s look at another example:
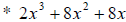
Step 1. The GCF is 2x, therefore the polynomial can be written as: 2x(x2 + 4x +
4)
Step 2. Now we have to factor a polynomial with three terms and it looks like a
perfect
square trinomial. Therefore, (x2 + 4x + 4) can be factored as (x + 2)2
Step 3. Check to see if factors can be factored further. If not, you have
reached the final
answer i.e.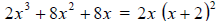
Long division/ Synthetic division method of factorizing
Higher order polynomials that cannot be solved using any of the above mentioned
methods, require the application of the rational roots test and long division.
This concept
will be explained using the following example:
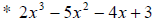
Since factoring by grouping does not work for this expression, we will use long
division.
Step 1. Rational roots test: Find the factors of the coefficients of the
constant term and
the highest order term and write these as p and q. In this case, p = 1,-1, 3, -3
and q = 1,-
1,2,-2. Now write 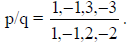 These give us a list of possible zeroes of the
These give us a list of possible zeroes of the
polynomial i.e. the polynomial will equal zero when
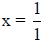 or
or 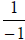 or
or or
or 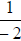 or
or or
or
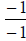 or
or 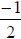 or
or 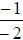 etc.
etc.
Use trial and error method to find which factor gives us
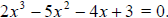
In this case it is seen that when 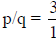 , i.e.
when x =3,
, i.e.
when x =3, 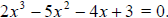
This tells us that one factor of the polynomial is (x-3).
Step 2. Synthetic division
For this, we will only use the coefficients of the polynomial
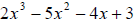 and
and
divide those by the factor ‘3’.
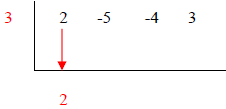 |
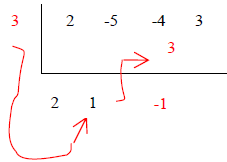
1. Pull down the first coefficient |
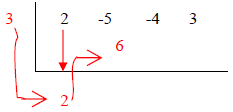 |
2. Multiply 3 and 2 and carry it over |
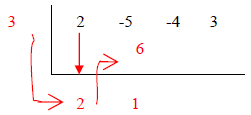 |
3. Add -5 and 6 |
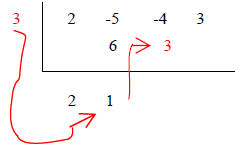 |
4. Multiply 3 and 1 and carry it over |
 |
5. Add -4 and 3 |
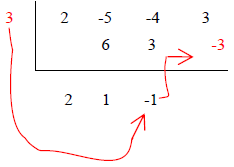 |
6. Multiply 3 and -1 and carry it over |
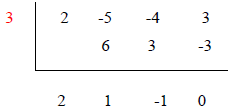 |
7. Add 3 and -3 |
| NOTE: This sum has to equal zero! If it does not, please re- do the calculations . Either there is an error in the division process or the selection of the initial zero. |
The coefficients of the quotient of this division are 2,
1, -1, and 0.
Since our problem was an order of 3. i.e.
![]() , our quotient will
be an
, our quotient will
be an
order lower i.e. our quotient will be of order 2.
The quotient therefore is given by: 2x2 + 1x -1.
The factorization so far is given by : (x-3)( 2x2 + x -1)
Step 3. Check to see if factors can be factorized further
2x2 + 1x -1 can be factored further.
We need to find two numbers such that their product is -2 and their sum is 1.
Let’s find
the factors of -2.
| Factors of -2 | 2,-1 | -2,1 |
| Sum of factors |
1 | -1 |
Our desired numbers are 2 and -1.
We will now re-write our trinomial : 2x2 + 2x −1x −1
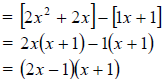
The final result is therefore: 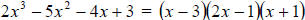
Try these examples on your own:
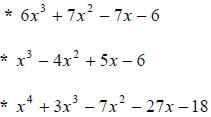
| Prev | Next |