Visual Fraction- Addition Teaching MethodJorge Garcia, Ph.D. †

Abstract

A visual method for adding fractions is introduced. The similarities between this and another method are studied. A formal definition is introduced in an intuitive and visual way. The multiplication is discussed as well as analogies between addition and multiplication with union and intersection of two sets. A final discussion on the philosophy of the method and a comparison with another method for adding fractions is presented here.

1 Introduction

The teaching of addition of fractions at an elementary school level has long a well known teaching challenge (Lappan-Bouck [4] and Lamon [3]). It is widely recognized that there are at least two major bottlenecks in the mathematics education of grades K-8: the teaching of fractions and the introduction of algebra.” ([5, Page 1]) There are several methods to approach the problem (Lamon [3]). Even though some have proved to be successful, there is still the need of minimizing the difficulty of the understanding of this addition process. This paper is intended to approach and present the problem in a uniquely different way.

The method proposed here focuses on a visual method that was discovered when trying to introduce fractions for the first time to a child in the second grade.

In Sections 2 and 3, I discuss the meaning of a fraction, its notation and the importance of understanding its value. In Section 4, pictures allow us to visualize the addition of fractions which is done in section 5. A comparison with other similar method of adding fractions is discussed in section 6, and finally the multiplication of fractions is discussed in section 7. The last sections are dedicated to the discussion on the importance of giving a concise answer when teaching of adding fractions. Analogies and the abstract meaning of the fractions are presented here .

2 What is one fourth?

What is one fourth? What is the actual value of one fourth? These are some of the typical questions a child might ask when he or she is exposed to the concept of a fraction for the first time. The most formal answers (which are believed to be the simplest) to these questions are presented in this section. The child is expected to have a concept of multiplication previous to any presentation of fractions.

There is an important number, it is called one, one unit, one unit of a value and its symbol is 1. Let's think of number four for a moment. Now there is a new number, called one fourth, that has the special property four of this make one. The four of this make one property consists of adding one number, the same number, the same number and the same number to obtain 1. In our case, by definition, one fourth has the property that if we add one fourth, one fourth, one fourth and one fourth together, we obtain 1. Another way of saying this is four times one fourth is the same as one unit. The value of this new number, one fourth, is still unknown; but the number one fourth has the above property that makes it different from others. It makes it unique. Its symbol is 1/4 and the four of this make one property can be written as in figure I.

Figure I
The four of this make one property in symbols and its simplified version

Among the numbers we knew so far (the integers), none of them satisfies the four of this make one property. We can try with number 2 for example, but it will impossible that 2+2+2+2 be equal to 1.

Let's now think of number 5, something similar happens. There is a number called one fifth that satisfies a property which is not called four of this make one anymore, no, the special property that one fifth satisfies is called five of this make one. The symbol for one fifth is 1/5. The five of this make one can be written as in

figure II.
Figure II The five of this make one property in symbols and its simplified version

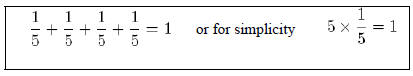
3 What is the true value of one fourth?

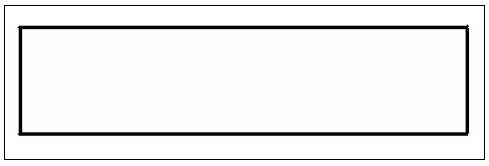
As we have met one fourth for the first time, we still do not know its true value. We will never find the true value of one fourth among the numbers we know. However, we can sense the value of one fourth as a small portion of one unit. Let's imagine that we have one cake, our birthday cake whose shape and size look like the figure 3.

Figure III
One Unit, one cake

Here our unit consists of a birthday cake of this size. One fourth of our birthday cake will be a small portion that has the special property four of this size make our birthday cake.

One fourth is not the small portion of the cake that looks like figure IV, since four of these pieces make just an amount like in the one shown in figure V, this amount has not the same size of our birthday cake.

Figure IV
A fake representation of one fourth

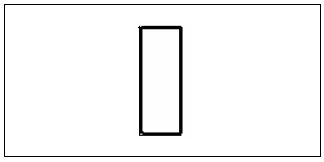
Figure V
Four fake pieces together

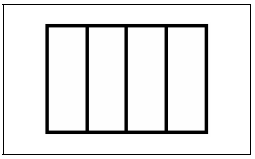
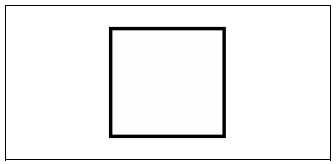
One fourth of our birthday cake looks like in figure VI.

Figure VI
A valid representation of one fourth

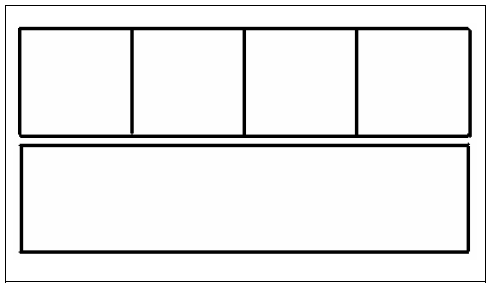
Indeed four of these pieces make an amount equal to the one of our birthday cake, as it can appreciated in figure VII.

Figure VII
Four valid pieces together make our whole birthday cake

4 Representing fractions as shading areas

Let's now fix or establish a size, a measurement, and clarify what our unit is; it will be a square, a particular square of any fixed size. The size is not really important as long as we agree that from now on, that will be the unit and it will not be changed. Three fifths will mean three single one fifth-pieces. Three fifths looks like shading one fifth and another one fifth and another one fifth together, like in the figure VIII.

Figure VIII
A colored representation of 3/5, the whole square represents our unit

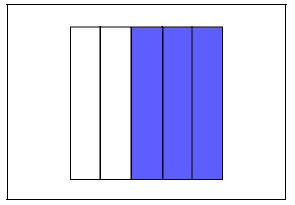
In figure VIII, just the shaded area is the one that represents three fifths and the whole piece represents one unit (one unit of cake for example). From now on, we will color transparent pieces of paper to represent fractions.

5 Adding fractions

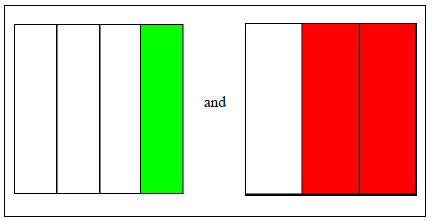
We add fractions of the type 1/12 and 3/12 in the following way, we have a single one twelfth and three singles one twelfth, therefore the sum of those will be four singles one twelfth, this is 4/12 (according to our definition of fractions). We will now study the addition of fractions of different type . We now face the situation where we wish to add two new numbers 1/4 and 2/3. Visually speaking, we want to add the quantities in figure IX.

Figure IX
We wish to add the quantities shown

We now put them together by superimposing both squares and rotate one of them ninety degrees. What we obtain is a grid of twelve little rectangles. The big square represents one unit, one unit of cake. The cake has been divided equally in twelve little parts. Some of them are red, other green and the other ones have a mixture of red and green (yellow) as in the figure X.

Figure X
The colored area represents the sum of 1/4 and 2/3. The yellow being a
combination of both , counts double

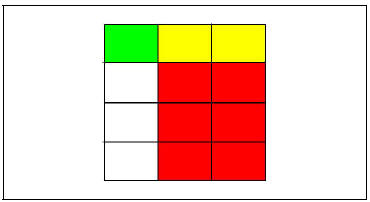
To find 1/4 + 2/3 we first count all the small rectangles that are colored red, we then add the ones that are colored green, we finally add the ones that have both colors, but these count double. We have then 1 (green) + 6 (red) + 2 (yellow) + 2 (yellow) = 11 colored pieces. Therefore the answer to 1/4 + 2/3 is 11 out of 12, in other words, 11 /12.

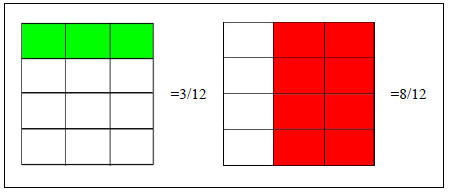
There is another way of approaching the same problem; in fact this is the justification on why the previous method works. If we just look at the superimposed squares and concentrate on the area that is or was green, then this area can be estimated as three out of twelve little rectangles, whereas the area that is or was red can be estimated as eight out of the twelve rectangles, as in the figure XI. Therefore the sum 1/4 + 2/3 can be seen as, 3/12+8/12, which is, 11/12.

Figure XI
Grid showing equivalences of the desired fractions

6 Comparing with Wu's method

H. Wu ([6, Page 55-56]) describes a geometrical representation of 2/3 that is similar to the one presented here. When trying to add 2/3 and 1/2, Wu combines the shaded areas in a horizontal way, and he divides each piece into six equal parts creating a grid with each piece. By aligning them horizontally, he uses these small rectangles as "yardsticks” to measure the combined area and then he proceeds to count. In figure XII, the sum of, the sum of 2/3 and 1/2 is illustrated via Wu's method ([6]) by aligning and dividing each square.

Figure XII
Wu’s representation and addition of 2/3 and 1/2.

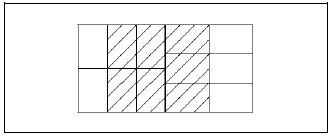
The method described by Wu is similar in the sense that a grid is created. It is different in the sense that he has to align the pieces, create the grid and do an analysis from there whereas in the method presented in this paper, there is a superimposition and the counting is direct.

7 Multiplication of fractions

There is an easy way to compute the product of two fractions via this method. It is understood that we define the product of two fractions a/b and u/v as a times b over v times u. Suppose we wish to multiply 1/4 and 2/3. Visually speaking, we want to multiply the quantities in figure XIII.

Figure XIII
We wish to multiply the quantities shown.

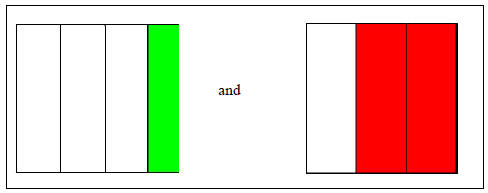
As before, we put them together by superimposing both squares and rotate one of them ninety degrees. What we obtain is a grid as in the figure XIV.

Figure XIV
The yellow area represents the product of 1/4 and 2/3

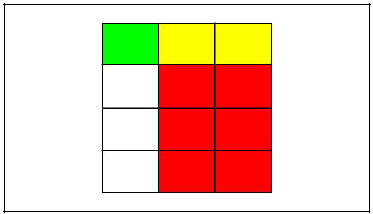
The result of the multiplication is the fraction represented by the yellow area, that is, 2/12. The reason for this is that when we superimpose the squares, we obtain a grid with as many rectangles as the product of the denominators of our fractions, in our case, 12. Horizontally we have as many colored strips as the numerator of one of our fraction and vertically we have as many colored strips as the numerator of our other fraction. In our case we have one green strip and two red strips. Hence the amount of rectangles whose colors overlap can be counted as the product of our numerators, in our case one green times two red produce 1x2 = 2 yellow rectangles.

ETA Cuisenaire Company ([1]) has produced the set Picture Grids (Fraction & Decimals ), Set of 60 ETA 020272.” This is a set of 60 translucent squared cards and each one of them has a fraction of it shaded with a given translucent color. Each card represents a fraction just as the representation described in this paper. The set of cards create the grid described here by superimposing them. The package comes with a written description on how to use the set, examples, pictures and problems. The written description provides a full explanation on how to compute the product of two fractions using the cards. However, the written description does not approach the addition of fractions at all.

8 Analogy between union and addition, intersection and multiplication

When we talk about the addition of two fractions, we really mean putting together both fractions. This is precisely what the union of two sets does, put together the sets. If the fractions are represented with colored areas, then the union of those areas will represent the sum of those fractions.

Analogously, the intersection of two sets provides the proportion of one set inside the other one. The intersection of two sets, in this case the colored areas, will represent a portion equal to the multiplication of our fractions.

In fact, if we make an algebraic ring out of a family of non-empty sets, the product of two sets will be given as the intersection and the sum of two disjoint sets will be given as the union of these.

9 Philosophy of the method and the importance of an abstract and formal answer

Wu ([6, Page 5]) defines a fraction as a division point on the real line . This is merely a geometrical description, a graphical definition . Lamon ([3]) writes: “As one moves from whole number into fraction, the variety and complexity of the situation that give meaning to the symbols increases dramatically. Understanding of rational numbers involves the coordination of many different but interconnected ideas and interpretations. There are many different meanings that end up looking alike when they are written in fraction symbol...” I think that intending to explain the meaning of a fraction as a result of combining old concepts such as the integers is a big mistake. People look and look for an interpretation of fractions in real life via numbers that they understand. A story that appeared at a newsletter for teachers at University of Rhode Island ([2]) tells that on the first day of the teaching career, an anonymous teacher defined a rational number to an eighth grade class as a number that can be expressed as a ration of integers. A student asked the teacher: What exactly are rations? How do rations differ from fractions? The teacher was not satisfied with the answers given to the student and the teacher consulted with some other teachers and texts. The result was confusion.

Wu ([6, Page 5]) mentions “...fractions tend to be discussed at the source, in the sense that attention is invariably focused on the interpretation of fractions in a real world setting. Since fractions are used in many contexts in many ways, students are led through myriad interpretations of a fraction from the beginning in order to get some idea of what a fraction is. At the end, a fraction is never defined and so the complexities tend to confuse rather than clarify...” Certainly the interpretations and the contexts on which fractions are involved are endless, however explaining a new concept in terms of the existing one is impossible. No combination or algebraic combination of integers will ever produce 1.

When we only know the natural numbers or the integers, the fractions are new numbers and we need to accept them as they are, new entities. They are defined in terms of their properties and therefore these properties make them unique. It is important to be able to recognize that the successful answers are the ones that are short, realistic, and formal. The best job that a teacher can do is trying to explain the formal definition in an intuitive and logical way to the children. That is why when a child asks me, what is one fourth? I answer; it is a new number that satisfies the property: four of this makes one.

Finally, the goal of applying the visual method described in this paper is not to gain expertise in all types of problems of addition of fractions (such as adding three fractions, subtracting fractions , etc.) but to gain intuition, clarity and formality about the concept of fractions and the sum of two of them.

† Jorge Garcia, Ph.D., California State University Channel Islands, USA

References

[1] E. Cuisenaire, Picture grids (fraction & decimals) set of 60 eta 020272, 500 Greenview Ct. Vernon Hills, IL 60061, (2005).
[2] C. M. T. in Grades 712, Newsletter of the mathematics, Department of the University of Rhode Island, 2 (1996), pp. 1{5.
[3] S. J. Lamon, Teaching Fractions and Ratios for Understanding. Mahwah, NJ: Lawrence Erlbaum Associates, 1999.
[4] M. K. Lappan, Glenda & Bouck, Developing algorithms for adding and subtracting fractions. The Teaching and Learning of Algorithms in School Mathematics. Morow, L. J. & Kenny, M. J. (editors), Reston, VA: National Council of Teachers of Mathematics., 1998.
[5] H. Wu, Some remarks on the teaching of fractions in elementary school, Department of Mathematics # 3840, University of California, Berkeley Berkeley, CA 94720-3840, (1999).
[6] , Chapter 2: Fractions., http://math.berkeley.edu/ wu/EMI2a.pdf, (2002). 13