Performing Arithmetic with Fractions
Adding and Subtracting
The simplest case when adding and subtracting fractions is the case when the
denominators of all fractions are the same. When adding fractions with like
denominators, simply add the numerators and keep the common denominator.
Example 1
To add the fractions 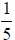 and
and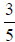 , add 1+3 to get 4 in the numerator, and retain the 5 in
, add 1+3 to get 4 in the numerator, and retain the 5 in
the denominator throughout the solution . So we have
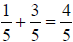 .
.
The first step in adding or subtracting fractions with unlike denominators is to
find a
common denominator of the fractions to be added . The easiest way to do this,
especially
when adding two fractions , is to multiply each fraction by the denominator of
the other.
For example, if you have two fractions, 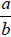 and
and
 , take
, take 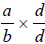 and
and 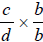 . The
. The
resulting fractions are  and
and
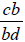 , and the denominators are the same.
, and the denominators are the same.
The final step when adding or subtracting fractions is simply to add (or
subtract) the
numerators and keep the common denominator. Continuing with the above example we
have 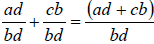 .
.
Example 2
Consider the fractions  and
and
 . To add
. To add  and
and  , first multiply
, first multiply
 by
by  and
and
 by
by
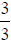 to get
to get 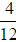 and
and 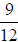 . Then add the numerators to arrive at
the final answer.
. Then add the numerators to arrive at
the final answer. 

In other cases, it may be possible to find a multiple of the two denominators
that is less
than the product of the two numbers . This is called the least common multiple or
LCM.
It often occurs that the LCM is one of the denominators.
Example 3
In the fractions 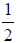 and
and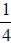 , the denominators have an LCM of 4, since 2 · 2 = 4 and
, the denominators have an LCM of 4, since 2 · 2 = 4 and
4 ·1 = 4 . In this case, it would be simpler to leave the second fraction as it
is and
multiply the first fraction by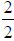 . So adding these two fractions we get
. So adding these two fractions we get

The reason we retain the denominator across and add only
the numerator is that the
numerator represents how many pieces of the whole exist; while the denominator
represents how many pieces the whole is divided into . The example above is shown
in
the figure below, where you can see that the above result is true.
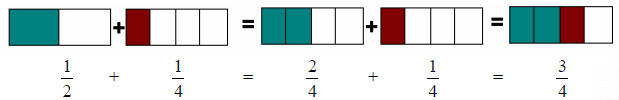
Figure 1
Multiplying
Before multiplying with fractions, it is important to understand the basic
concepts behind
multiplication with integers. As shown in the figure below, multiplication may
be
interpreted as the area of a rectangle where the quantities multiplied are the
length of the
sides and the resulting quantity is the value of the area inside. The lengths of
the sides
below are 2 and 3. When these are multiplied together, the area inside is equal
to 6 unit
squares. So we see that 2 · 3 = 6 .

Figure 2
The process is similar for multiplying fractions. In this case, we allow the
denominator
to be the whole length of the side and the numerator to be the portion of the
side
represented by the fraction.
Example 4
This time, lets multiply the fractions![]() and
and
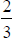 .
.
The multiplication is represented in figure 3 to the
right.
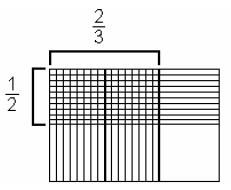
In this case, notice that the lengths of the sides, 2 and
3, are represented by the
denominators and the total area of the figure is the denominators multiplied
together.
In this case 2 * 3 = 6 unit squares. Now, the lengths of the shaded sides, 1 and
2, are
represented by the numerators and the area of the shaded area is the numerators
multiplied together. In this case, 1 * 2 = 2 unit squares. So, the final result
is two
unit squares out of six unit squares, represented by the fraction
 , where 2 represents
, where 2 represents
the shaded region and 6 represents the whole region.
This means that when multiplying fractions, a common denominator is not
required.
Instead, multiply the denominators to get the total number of parts and multiply
the
numerators to get the number of parts actually used.
In other words, if you have fractions
![]() and
and
![]() , multiplying them
together results in the
, multiplying them
together results in the
fraction . As in the example above,
. As in the example above,
 .
.
Dividing
It is also important to understand the basic concept behind dividing before
dividing
fractions. Consider the division problem 6 ÷3. The figure below shows how
dividing six
figures into groups of three results in the answer of two.
| 6 men divided into two group of 3 men each makes 2 groups.
|
Figure 4
Now, when dividing with fractions, the result is similar.
Example 5
Consider the problem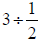 . Then you would divide
the three units into groups of
. Then you would divide
the three units into groups of
half units, as shown in figure 5 below.
| Each circle represents one of the 3 units, and the three altogether are divided into 6 groups of half a unit each.
|
Figure 5
In this case, we see that
![]() results in six total
units.
results in six total
units.
Looking carefully, you may notice that 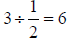 is
the same as
is
the same as  . This is true in
. This is true in
all cases. Given the calculation 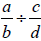 , take the
reciprocal of the second fraction (or a
, take the
reciprocal of the second fraction (or a
denominator if the two fractions are expressed as a ratio ), and then multiply
the two
resulting fractions together. The result in this case is
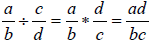 .
.
Example 6
Calculate 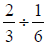 . Remember to simplify the
fraction when you are finished.
. Remember to simplify the
fraction when you are finished.
Solution: 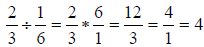
In a diagram,
![]() means that you have 2
pieces
means that you have 2
pieces
divided into groups of 3, so you have three spaces for
pieces with only 2 filled, as shown to the right.

3 spaces and 2 are filled
Next, we divide each piece into groups of size
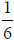 each, resulting in 12 total pieces as
each, resulting in 12 total pieces as
shown in the diagram below.

2 pieces divided into groups
of size one sixth results in
12 pieces
Since there are 12 pieces in 3 spaces or units, we see
that the resulting fraction is 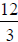 , which is the
same as
, which is the
same as
the result we found in the calculation above .
| Prev | Next |