Polynomials and Rational Functions
Find the vertex of the parabola :
1. x2 + 3x + 3
Graph by hand by finding the vertex, axis of symmetry, x and y intercepts,
leading
coefficient , and extra points. Give the domain and range of the function:
2. x2 – 7x + 12
Find the zeros of the function , state the multiplicity, and state if the line
crosses or touchs
the x-axis:
3. 2x3 – 4x2 + 2x
Prove the function has a zero within the interval by using the Intermediate
Value
Theorem:
4. f(x) = x4 – x3 + 3x2 – 5; (0, 2)
Divide using long division:
5. (6x2 + 3x4 – 3x + 2) ÷ (x + 3)
Divide using synthetic division :
6. (7x – 5x5 + 4x2 –8) ÷ (x + 3)
List all possible zeros and find all zeros of the function.
7. x3 – x2 – x – 2 = 0
Find all zeros of the function by using the Rational Zero Theorem, Descartes'
Rule of
Signs and quadratic formula .
8. 4y5 + 12y4 – 41y3 – 99y2 + 10y + 24 = 0
Graph the function by finding horizontal, vertical, and/or slant asymptotes,
symmetry, x
and y intercepts , and extra points if possible.
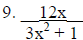
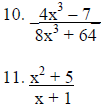
Solve the inequality and write answer in interval notation.
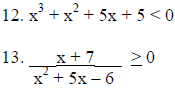
Solve :
14. The cost of a product is a function of the number of products produced as
given in the
equation where x is the number of products produced and C(x) is in dollars.
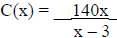
a. Find and interpret C(20), C(40), and C(60).
b. Where is the vertical asymptote?
c. Graph the function .
| Prev | Next |