Precalculus Course Objectives
Course Goal: The goal of Math 151: Precalculus is
to prepare each student for
Calculus Analytic Geometry I. A student well prepared for calculus will be able
to model
real-world problems and analyze their quantitative aspects using strong
algebraic and
trigonometric skills.
Course Objectives:
Throughout the semester, the student will:
1: Identify various functions, including square root , cubic, and
piecewise-defined
functions, and perform transformations and operations on known functions to
create new
functions. Construct mathematical models from real-world word problems.
2: Identify quadratic, polynomial, and rational functions and analyze their
graphs. Solve
polynomial and rational inequalities. Evaluate real-world problems using
rational
function models.
3: Find the real zeros of polynomial functions using various theorems.
4: Identify one-to-one functions and find their inverses. Explore exponential
and
logarithmic functions and use their properties to model and solve real-world
problems
involving compound interest and uninhibited growth/decay.
5: Explore angles and their measure. Establish the value of trigonometric
functions using
right triangle trigonometry. Analyze properties of the graphs of trigonometric
functions
and apply transformations and shifts to sinusoidal graphs.
6: Explore inverse trigonometric functions. Prove identities involving
trigonometric
functions and use them to solve trigonometric equations.
7: Solve real-world applications by creating right triangles and using
trigonometric and
inverse trigonometric functions.
Student Learning Outcomes by chapter:
Test questions listed will assess the student’s achievement of the desired
learning
outcomes. On completion of Math 151, the student should possess the ability to:
1:
• Construct the graph of new functions by translating old ones (shifting,
stretching, reflecting)
Ex. Write a function from its graph using transformations (shifts).
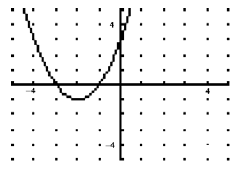
• Analyze real-world situation by creating an equation
for a piecewise -defined
function and graph it
Ex. At Car Rental R Us the following rate schedule applies for weekly rental of
a
car.
| Weekly rental fee | $135.00 |
| Per mile charge | |
| 0 to 250 miles | $0.49/mile |
| Over 250 miles | $0.29/mile |
(a) What is the charge (rounded to the nearest cent) for a weekly car
rental if the car was driven 175 miles?
(b) What is the charge (rounded to the nearest cent) for a weekly car rental if
the car
was driven 475 miles?
(c) Construct a piece-wise function that relates the weekly charge C for x miles
driven.
(d) Graph the function, label and scale the axes and several points on your
graph.
• Formulate a composite function and find its domain
Ex. Given the functions 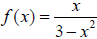 , and
, and
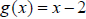 find and simplify
find and simplify
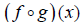 .
.
2:
• Use the maximum/minimum value of a quadratic function to optimize applied
problems
Ex. A landscape engineer has 200 feet of border to enclose a rectangular pond.
What dimensions will result in the largest pond?
• Evaluate applied problems using rational functions
Ex. The cost function for manufacturing Flash Memory cards is estimated to be:
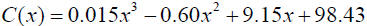
Where C(x) is the daily cost, and x is the number of flash
memory cards manufactured
per day.
Economists define the average cost function as
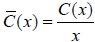
a) Find the average cost function and state the
domain.
b) What is the average cost (to the nearest penny) of manufacturing 50 flash
memory
cards per day?
c) How many flash memory cards would need to be printed per week if the average
cost per flash memory card is $20? Round your answer to the closest integer.
d) Find the number of flash memory cards manufactured per day that should be
produced to minimize the average cost. Round your answer to the closest integer.
e) What is the minimum average cost, to the nearest penny?
• Solve a quadratic equation.
Ex. Solve the equation. Find exact values where possible, otherwise round to two
decimal places . 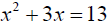
• Determine where a function is increasing/decreasing, and identify the
domain,
vertical/horizontal/oblique asymptotes of a rational function
Ex. The concentration C (in milligrams) of a certain drug in a patient’s
bloodstream
t minutes after injection is given by 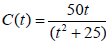 Using
your graphing
Using
your graphing
calculator, graph C (t) to answer the following questions.
a.) What happens to the concentration of the drug as t increase?
b.) Determine the time at which the concentration is highest.
c.) What is the highest concentration?
d.) Determine the interval (s) where the function is increasing.
e.) Determine the interval (s) where the function is decreasing.
f.) What is the horizontal asymptote of C (t)?
If the drug is to be re-administered when the concentration decreases to 2
milligrams,
how many minutes after the initial dose is the drug re-administered?
• Solve polynomial and rational inequalities and graph them
Ex. Solve the inequality and graph the solution set on the real number line.
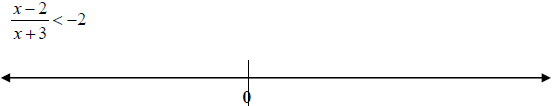
3:
• Calculate the real zeros of a polynomial function by applying Descartes’ Rule
of
Signs and the Rational Zeros Theorem, and use the zeros and end behavior to
graph the polynomial
Ex. Answer the following to analyze the graph of the polynomial function
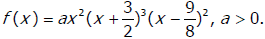
a. What is the y- intercept ?
b. Find the exact zeros and complete the table for each zero of . ()
| Zeros | Multiplicity |
c. What power function does f (x) resemble for large
values of l x l?
d. Using the information from a, b, and c), sketch the graph below. Label your
axes.
Label the points found in parts a and b.
• Apply the remainder theorem and factor theorem to determine if a function
has
specified zeros
Ex. Find k such that  has the factor x-2
has the factor x-2
4:
• Calculate the time required to double or triple money or determine the future
value of a lump sum of money
Ex. How much will you have after 5 years if you invest $20,000 earning 4.75%
compounded a. Monthly and b. Continuously. Round your answers to the nearest
cent.
• Develop equations of populations that obey the law of uninhibited growth or
decay and predict future populations
Ex. The half-life of a certain radioactive substance is about 2,750 years. If 50
grams is
present in a sample of soil now, how much will be present in 500 years? Round
your
answer to the second decimal place.
• Calculate the inverse of a function and construct its graph
Ex. The function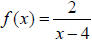 is one-to-one. Find the
inverse of in explicit
is one-to-one. Find the
inverse of in explicit
form.
• Construct exponential expressions from logarithmic
expressions and vice versa
to solve exponential and logarithmic equations. Using properties of logarithms
to
create a single logarithmic expression from a sum/difference of logarithms to
solve logarithmic equations.
Ex.
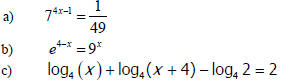
5:
• Acquire an angle measure in radians by converting from degrees to calculate
the arc length of a circle and the area of a sector of a circle
Ex. The minute hand of a clock is 6 inches long. How far does the minute hand
move in 15 minutes? What is the area of the sector covered by the minute hand in
those 15 minutes?
• Establish the remaining trigonometric functions given the value of one of
them
Ex. Find the exact value of the remaining trigonometric functions given that tan
θ=3
and sin θ<0. Include a sketch to explain your work.
• Acquire the value of trigonometric functions of acute angles (including 30,
45, 60
degree angles) and general angles
Ex. Find the value of each remaining trig function of the acute angle given that
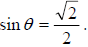
• Apply the fundamental identities to simplify and
solve equations
Ex. 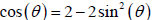 on the
interval
on the
interval 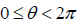
• Apply the complementary angle theorem to acquire the
value of trig functions
Ex. Find the exact value without using a calculator: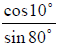
• Apply coterminal angles to find the exact value of a
trig function
Ex. Find the exact value without using a calculator: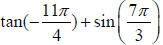
• Identify the reference angle and apply the theorem on
reference angles
Ex. Find the exact value without using a calculator:
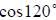 .
.
• Determine the domain, range, amplitude, and period of
sinusoidal trigonometric
functions. Using given data, create a sinusoidal function.
Ex. Write an equation in sine and cosine for the following graph. Two equations
are
required.
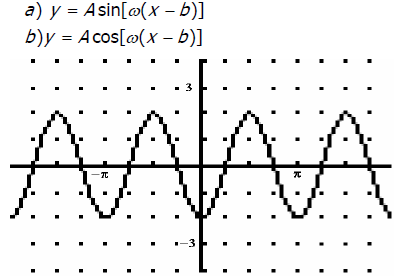
6:
• Calculate the exact value of the inverse sine, cosine, and tangent functions
Ex. Find the exact value. 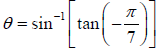
• Verify identities
Ex. Establish the identity:
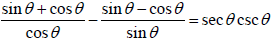
7:
• Solve right triangles
Ex. Solve the right triangle.
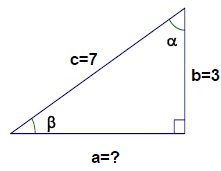
Specify degrees or radians.
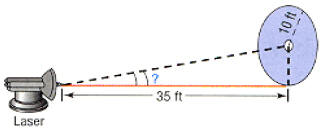
• Assess applied problems using right triangles
Ex. A laser beam is to be directed through a small hole in the center of
a circle of radius 10 feet. The origin of the beam is 35 feet from the circle
(see the figure). At
what angle of elevation should the beam be aimed to ensure that it goes through
the hole?
| Prev | Next |