Precalculus I Lecture Notes
Wed 5 Nov — Review for Exam 3 on Cpt 3 and 4
Next two midterms in 125 Willey Hall rather than here.
Exam will cover material from chapters 3 and 4, but you still must remember
everything from all
previous work ! Here is an outline of topics you should know:
3.1 Linear Functions and Their Properties
Graph linear functions
y = mx + b
Average Rate of Change from x = a to x = c is the slope of the secant line through the two points.
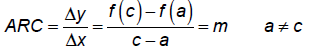
Determine whether a linear function is increasing, decreasing, or constant
Applications of linear functions (word problems)
3.3 Quadratic Functions and Their Properties
Define quadratic function
f (x) = ax2 + bx + c, a ≠ 0
Graph a quadratic function using transformations
EX: Using transformations, graph
f (x) = - (x - 3)2 - 2 Start with: g (x) = x2
The negative reflects the graph about x-axis:
h(x) = -x2
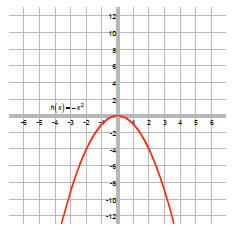
The - 3 shifts the graph right 3 units: j (x) = - (x - 3)2
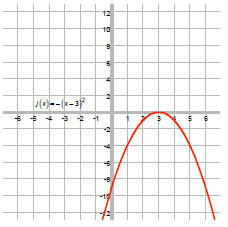
The – 2 shifts the graph down 2 units: f (x) = - (x - 3)2 - 2
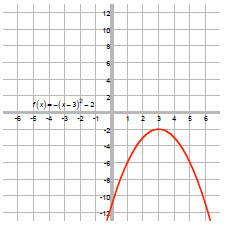
As a check, find vertex: The equation is in the form
f (x) = a(x - h)2
+ k so the vertex, (h, k) should be at (3, –2).
The x- intercepts are at :
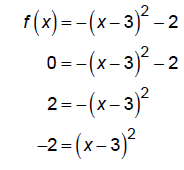
This has no real solution so there are no x-intercepts.
The y-intercept is at
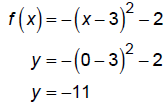
It all checks.
The highest or lowest point is the vertex. The x coordinate of the vertex is
at
xvertex
= -b/2a
y-coordinate is
yvertex = f (xvertex)
Maximum or minimum value of a quadratic function is at vertex.
The graph of a quadratic function is a parabola.
Axis of symmetry is at
x = xvertex
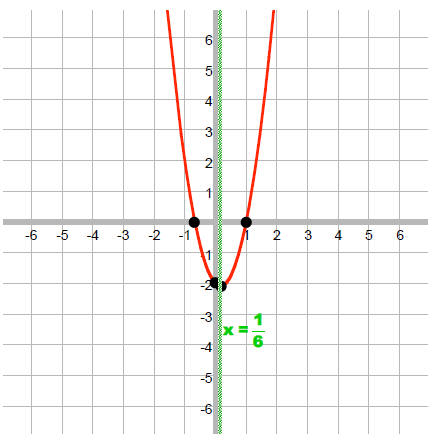
EX: Given: f (x) = 3x2 - x - 2 Find:
x-int Ans: -2/3 and 1
y-int Ans: -2
vertex
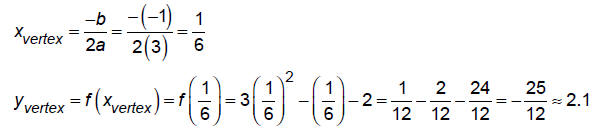
line of symm:
x = xvertex so axis of symmetry is
x =1/6
Domain: All real numbers
Range: Lowest value f takes on is at the vertex
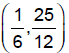 so range is
so range is
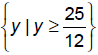
3.4 Quadratic Models & Building Quadratic Functions (word problems).
pg 160 #44 is a HW problem that people are struggling with so here it is:
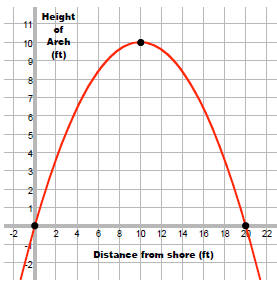
A horizontal bridge is in the shape of a parabolic arch. Construct a function
that gives the height of
the lower part of the bridge as a function of the distance from the shore. The
max height of the
bridge is 10 ft and the width at the level of the river is 20 ft.
1. Read the problem several times carefully until you fully understand it.
2. Draw a diagram if appropriate.
3. Identify any formulas you might need (e.g., area, perimeter, simple
interest ).
f (x) = ax2 + bx + c of f (x) = a(x - h)2 + k
4. Assign a variable to represent what you are looking for.
We want the height as a function of the distance from the shore. So, lets
define:
x = distance (ft) from shore.
5. Express any other unknown quantities in terms of your variable.
h(x) = height of bridge above water.
6. Write an equation that models a relationship between your
expressions .
h(x) = ax2 + bx + c or h(x) = a(x - h)2 + k
Place a coordinate system so that the origin is at the left side
of the arch where it touches the water.
The vertex is at (10, 10).
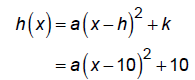
We also know the parabola crosses the x-axis at (0,0). So, we can solve for a .
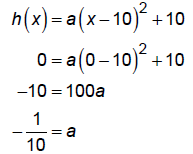
7. Solve the equation.
8. Write the final answer, including units.
So, we have: 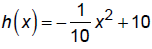
9. Check the answer with the facts in the problem.
3.5 Inequalities Involving Quadratic Functions
Solve inequalities involving a quadratic function
Solve: x2 < x + 2
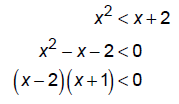
Graph the parabola by plotting the x-intercepts and noting it opens up.
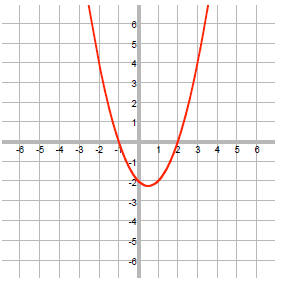
From the graph, we can see that f(x) < 0 for -1 < x < 2.
We could also do this algebraically by breaking up the number line into
intervals

trying test points and seeing where f(x) is negative.
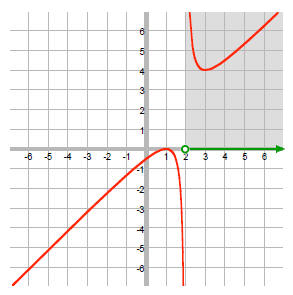
4.1 Polynomial Functions and Models
Degree
Power functions
Graph polynomial functions using transformations
Identify real zeros of polynomial functions and their multiplicities
Behavior near a zero
Turning points = n - 1
End behavior
Analyze the graph of a polynomial function
Graph:
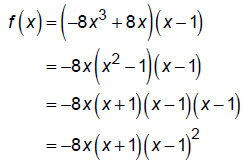
Find x- and y-intercepts.
x-int: x = 0 cross, -1 cross, 1 touch (mult is 2)
y-int: y=0
End behavior: graph looks like
f (x) = axn .
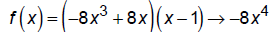 which is like an upside down parabola.
which is like an upside down parabola.
4.2 Properties of Rational Functions
Domain
Vertical asymptotes
Horizontal or oblique asymptotes
4.3 Graph of a Rational Function
Analyze the graph of a rational function, including holes.
Applications of rational functions (word probs)
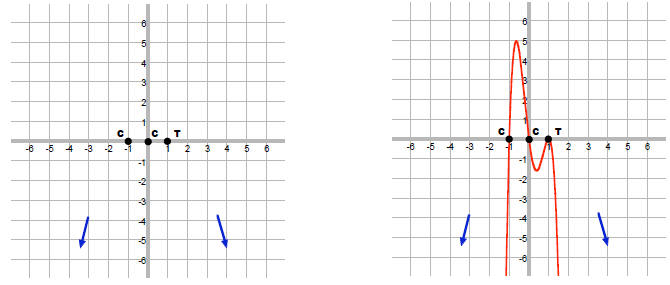
Graph:
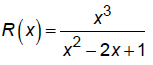
Domain:
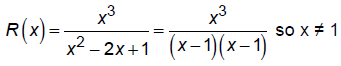
Cannot reduce so no "hole" in graph.
y-int:
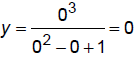
x-int:
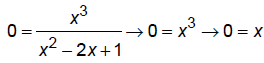
Multiplicity of x -intercept is 3, which is odd, so graph CROSSES here.
vert asym: The line x = 1. This has multiplicity 2 so graph approaches each side
in same direction
(both up or both down)
hor or oblique asym: (degree of p) = (degree of q + 1) so there is an oblique asym.
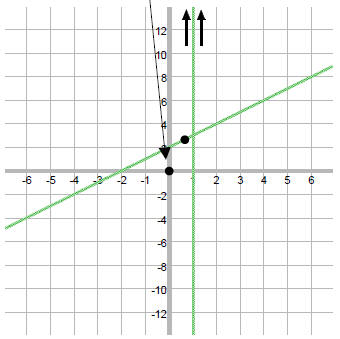
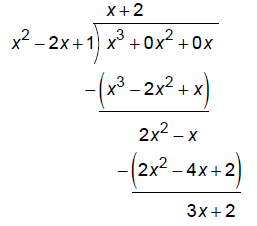
So, OH is y = x + 2
See if graph crosses the OH:
R(x) = y
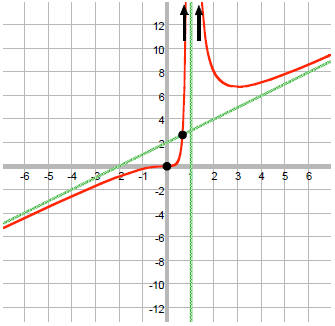
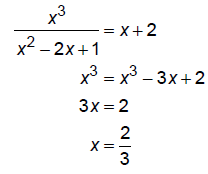
Yes, so the graph crosses the OH when x = 2/3.
Graph:
4.4 Polynomial and Rational Inequalities
Solve polynomial inequalities
Solve rational inequalities
EX: Solve:
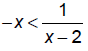
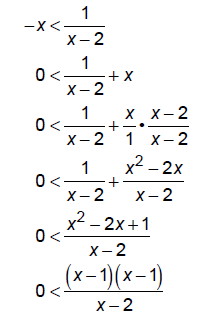
Break up number line into intervals and try test points:
Interval :

| Try x = | 0 | 3/2 | 3 |
| Get f = | 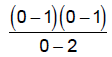 |
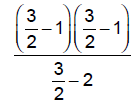 |
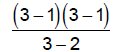 |
| Simplify : | -1/2 | -1/2 | 4 |
| f (x) > 0 | no | no | yes |
So, solution is
{x | x > 2}
| Prev | Next |