Prerequisite Study Sheet for MATH 1316
In MATH 1316, one learns how to work with trigonometric functions, identities, equations, and applications of all of these. Students who wish to take scientific calculus must learn the material in MATH 1316 and MATH 2412, Precalculus, to prepare for MATH 2413, Calculus I. To begin the trigonometry course, it is necessary that you have completed the prerequisite for the course (one semester of high school trigonometry or precalculus or College Algebra or the equivalent and that you recall most of the geometry and how to use most of the algebraic techniques you have already learned. There is little or no review of algebra in the trigonometry course.
The following problems provide a quick review of this algebra for students who have completed the prerequisite. The answers are listed at the end. If you find any of these that you do not know how to do correctly, you need to do one of two things before you enroll in MATH 1316:
1. Get an algebra book (at the Intermediate Algebra or College Algebra level) and review these topics until you can do all of these problems. If you do not have a book, you may check one out of the LRS, buy a non-current textbook at a used book store, buy an algebra book in the Schaum's Outline Series, or buy a current textbook.
2. If you are unable (or don't have time) to learn these topics by reviewing on your own, you need to take an algebra course to refresh your algebra skills. Students who have had two years of high school algebra or the equivalent and are able to do only about 2/3 of these correctly may choose to take MATH 1314 (College Algebra) to prepare for MATH 1316.
Problems:
1. A ladder is leaning up against the side of a house. If the bottom of the ladder is 7 feet from the house and the ladder is 14 feet long, how far up the side of the house is the top of the ladder?
2. Recall the geometrical theorem that says that the ratios of the corresponding sides in similar triangles are equal. Suppose that you want to measure the height of a building. To do this, you measure the building's shadow and find that it is 50 feet long. You also measure the shadow of a 4-foot stake and find its shadow to be 3.5 feet long. How tall is the building?
3. Find the distance between the two points: (-1, 5) and (2, 12).
4. Find an equation for the line through the points
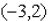 and
and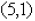 .
.
5. Sam Jones has a total of $5000 invested in two accounts, one at 5% per year and the other at 7% per year. The total amount of interest earned each year is $320. How much is in each account?
6. The price of a microwave oven has been discounted by 15%. The sale price is $339.15. What is the original price of the microwave oven?
In 7-14, solve for x .
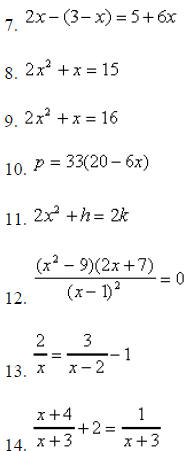
In 15 and 16, tell whether each system has none , only one, or many solutions. If
it has only one, solve it.
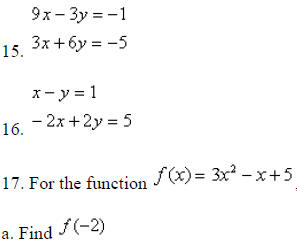
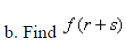
18. Divide and simplify :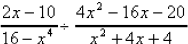
19. Graph 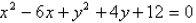
20. Graph 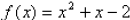 on the
interval
on the
interval 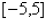 .
.
21. If you're given an equation with variables x and y and you want to find the x and y intercepts of the graph of the equation , how should you do it?
22. Simplify: 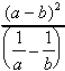
23. Simplify: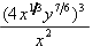
24. Simplify: 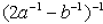
25. Solve for r: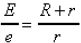
Topic names and answers: (If you find misprints in the answers, please report them to Mary Parker.)
1. Pythagorean theorem: height is
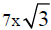
2. Similar triangles: 57.14 feet
3. Distance formula: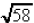
4. Straight lines: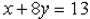
5. Interest word problem: $1500 at 5%, $3500 at 7%
6. Percentages: $399
7. Linear equations :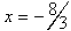
8. Quadratic equations , factorable: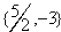
9. Quadratic equations, general: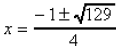
10. Formulas or literal equations (linear):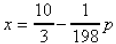
11. Formulas or literal equations (quadratic):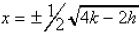
12. Rational equations: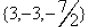
13. Rational equations: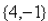
14. Rational equations (notice how to check for extraneous
roots ): 
15. Systems of equations: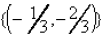
16. Systems of equations: No solution
17. Function notation: 19 and
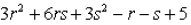
18. Factoring and rational expressions:
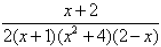
19. Graphing circles: circle, center at
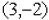 , radius 1
, radius 1
20. Graphing quadratic functions: a parabola , opening upward, with x intercepts at 1 and -2.
21. Graphing lines If you have the graph, simply look for
the intercepts. With the equation, set 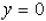 and
solve for x to find the x-intercepts. Set
and
solve for x to find the x-intercepts. Set 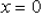 and
solve for y to find the y-intercepts.
and
solve for y to find the y-intercepts.
22. Rational expressions :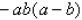
23. Rational exponents :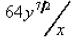
24. Rational exponents: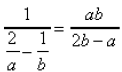
25. Formulas or literal equations (rational):
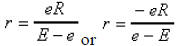
| Prev | Next |