Rational Expression
1 Review Factoring
Factoring plays a big part of simplifying rational expressions. So we first give
a
short review of factoring.
When two integers are multiplied together, the answer is called a product.
The integers that were multiplied together are called the factors of the
product.
For example, 3 and 6 are factors of 18.
Factoring is an important algebraic skill . The following are some basic fac-
toring techniques you should know.
• Factor out a common monomial (or binomial) factor. (The key idea in this
process is to recognize the monomial (or binomial) factor that is common
to all terms), e.g., the greatest common monomial factor to 10x2y3 and
15xy2 is 5xy2.
• Factoring by applying the difference-of-two- squares pattern . (e.g., a2 -
b2 = (a - b)(a + b))
• Factoring by applying the sum -of-the-two- cubes or the difference -of-two-
cubes pattern. (e.g., a3 + b3 = (a + b)(a2 - ab + b2), and a3 - b3 =
(a - b)(a2 + ab + b2))
• Factoring of trinomials into the product of two binomials . (The perfect-
square-trinomial pattern is a special case of this technique.) For example,
let's see what is involved with factoring 2x2 - x - 6. First, check to see
if all of the terms share a common factor which may be removed. If each
term can be factored before you begin, your work will be easier. The terms
in this problem do not have a common factor. Second consider all of the
possible factors of the leading coefficient, 2x2. In this problem we only
have one choice, 2x and x. So we can start with:
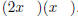
Third consider all of the possible factors of the last
term, -6. The possible
answers are: +6 and - 1; -6 and + 1; +3 and - 2; -3 and 2. You need
to test each of these pairs to see which will yield the correct middle term.
Answer: (2x + 3)(x - 2).
2 Simplifying Rational Expressions
After this class, you should be able to:
• Find the domain of a rational expression .
• Simplify a rational expression.
Definition A rational expression is one that can be written in the form
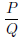
where P and Q are polynomials and Q does not equal 0.
An example of a rational expression is:
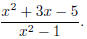
2.1 Domain of a Rational Expression
With rational functions, we need to watch out for values that cause our denom-
inator to be 0. If our denominator is 0, then we have an undefined value. So,
when looking for the domain of a given rational function, we use a back door
approach. We find the values that we cannot use, which would be values that
make the denominator 0. For example the rational expression
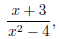
is undefined for x = 2 and x = -2, but defined for x = -3.
2.2 Fundamental Principle of Rational Expressions
Theorem 2.1 For any rational expression 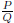 , and
any polynomial R, where,
, and
any polynomial R, where,
R ≠ 0, then
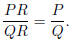
In other words, if you multiply the EXACT SAME thing to
the numerator and
denominator, then you have an equivalent rational expression. This will come
in handy when we simplify rational expressions, which is coming up next.
2.3 Simplifying ( or reducing ) a Rational Expression
Step 1: Factor the numerator and the denominator.
Step 2: Divide out all common factors that the numerator and the denominator
have.
Example: Simplify the rational expression
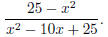
Step 1: Factor the numerator and the denominator
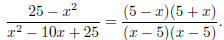
(factor the difference of squares in the numerator and
factor the trinomial in
the denominator)
AND
Step 2: Divide out all common factors that the numerator and the denomi-
nator have.
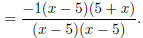
(factor out a -1 from (5 - x)).
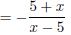
(divide out the common factor of (x-5), and the rational
expression simplified).
Note that 5 - x and x - 5 only differ by signs , in other words they are
opposites
of each other. In that case, you can factor a -1 out of one of those factors and
rewrite it with opposite signs, as shown above.
3 Homework
(section 4.1) 7, 8, 15, 17, 24, 25, 29, 30, 35, 37, 40, 51, 52, 53, 58, 60, 63,
64, 65,
67.
| Prev | Next |