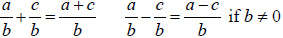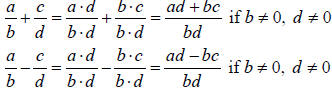Rational Expressions
Objective 1 Reduce a Rational Expression to Lowest Terms
If we form the quotient of two polynomials, the result is called a rational
expression .
Some examples of rational expressions are
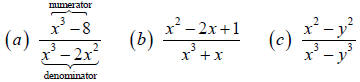
Expressions (a), and (b) are rational expressions in one
variable , x , whereas (c) is a rational expression in two
variables, x and y.
When the numerator and denominator of a rational expression contain no common
factors (except 1 and −1), we say
that the rational expression is reduced to lowest terms , or
simplified.
The polynomial in the denominator of a rational expression cannot be equal to 0
because division by 0 is not
defined.
For example, for the expression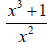 , x cannot
take on the value 0 . The domain of the variable x is {xl x ≠ 0}.
, x cannot
take on the value 0 . The domain of the variable x is {xl x ≠ 0}.
Example 1 Reducing Rational Expressions to Lowest Terms
Reduce each rational expression to lowest terms.
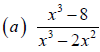
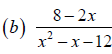
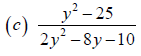
Objective 2 Multiplying and Dividing Rational Expressions
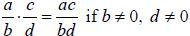 |
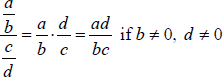 |
Example 2 Multiplying and dividing Rational
Expressions
Perform the indicated operation and simplify the result . Leave your answer in
factored form.
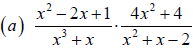
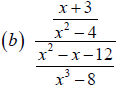
Objective 3 Adding and Subtracting Rational Expressions
If 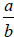 and and
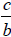 are two rational expressions, then are two rational expressions, then
|
Example 3 Adding and Subtracting Rational
Expressions with Equal Denominators
Perform the indicated operation and simplify the result. Leave your answer in
factored form.
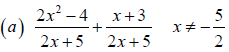
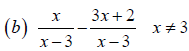
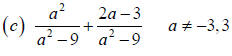
Example 4 Adding Rational Expressions Whose
Denominator Are Additive Inverses of Each Other
Perform the indicated operation and simplify the result. Leave your answer in
factored form.
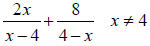
| If
|
Example 5 Adding and Subtracting Rational
Expressions with Unequal Denominators
Perform the indicated operation and simplify the result. Leave your answer in
factored form.
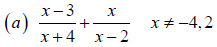
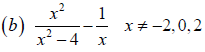
Objective 4 Use the Least Common Multiple (LCM) Method
The least common multiple (LCM) of two or more polynomials is the polynomial of
least degree and least positive
constant factor that has each of the given polynomials as a factor.
The least common denominator (LCD) of two or more rational expressions is
the LCM of their denominators.
To find the LCM of two or more polynomials you first factor each of the
polynomials completely. The LCM will be
the product of all the different factors , each factor occurring in the product
the greatest number of times that it occurs
in the complete factorization of any one of the given polynomials.
Example 6 Finding the Least Common Multiple
Find the least common multiple (LCM) of the following pair of polynomials
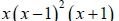 and
and
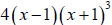
Example 7 Using the Least Common Multiple to Add
Rational Expressions
Perform the indicated operation and simplify the result. Leave your answer in
factored form.
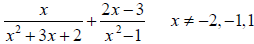
Example 8 Using the Least Common Multiple to
Subtract Rational Expressions
Perform the indicated operation and simplify the result. Leave your answer in
factored form.
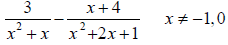
Objective 5 Simplify Complex Rational Expressions
When sums and/or differences of rational expressions appear as the numerator
and/or denominator of a quotient, the
quotient is called a mixed quotient (complex fraction).
For example,
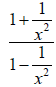 and
and
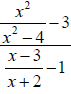
are mixed quotients.
To simplify a mixed quotient means to write it as a rational expression
reduced to lowest terms.
Example 9 Simplifying a Mixed Quotient (Using Method 2)
Simplify: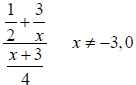
Example 10 Simplifying a Mixed Quotient (Using
Method 1)
Simplify: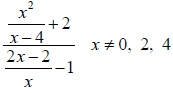
| Prev | Next |