Quadratic Formula
Warm-up
1. A line parallel to the x-axis intersects a parabola
exactly once, at the point (1, 1).
What special point on the parabola is (1, 1)? It is the vertex.
2. Find the vertex and state if it is a maximum or minimum: y = 3x2 - 6x + 7 (1,4), minimum
3. State how to translate the graph of y = 0.5x2 to produce y = 0.5(x - 1)2 + 5. Right 1, up 5
4. Solve:
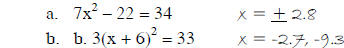
5. Solve:

Today we will:
1. Use the quadratic formula to solve quadratic equations
Tomorrow we will:
1. Continue with section 4-5.
4-5 The Quadratic Formula
You can find exact solutions to some quadratic equations by factoring.
However, not all quadratic equations are factorable , so we use the quadratic
formula.
The quadratic formula will enable you to solve any quadratic equation – it
always works!
The Quadratic Formula
For any quadratic equation in standard form ax2 + bx + c = 0 , the exact
solution (roots) are
given by:
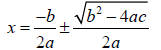
What can we tell about a graph in standard form from the quadratic formula?
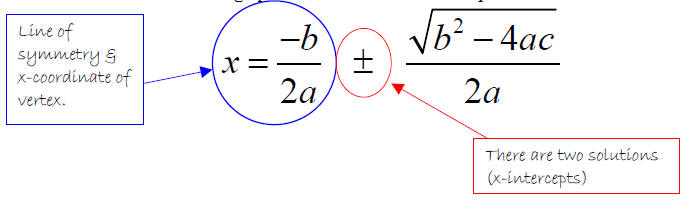
Remember to put the equation in standard form to solve. ax2 + bx + c
Example 1
Solve x + 4 = x2
Solution
Put in ax2 + bx + c = 0 first!
x2 - x - 4 = 0 ← Get the equation in standard form…
So…
a = 1, b = -1, and c = -4
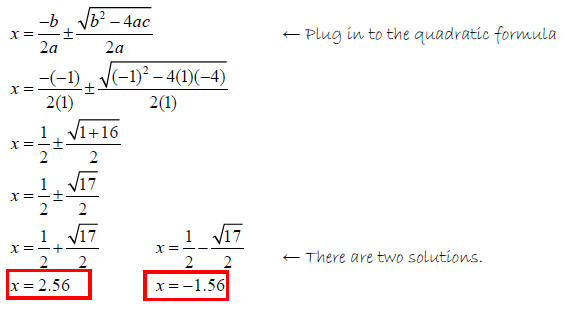
Example 2
Solve 5x2 + 6x +1 = 0
Solution
5x2 + 6x +1 = 0
The equation is in standard form…
So…
a = 5, b = 6, and c = 1
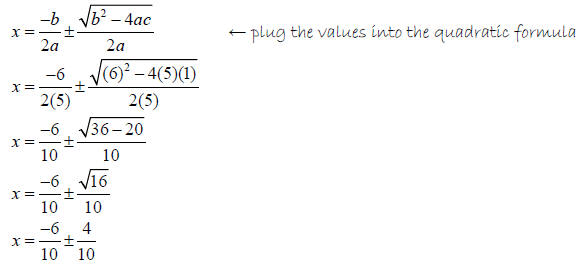
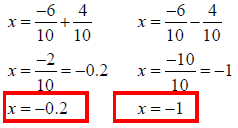
Example 3
Solve x2 - 4x + 3 = 0
Solution
The equation is in standard form…
So…
a = 1, b = -4, and c = 3
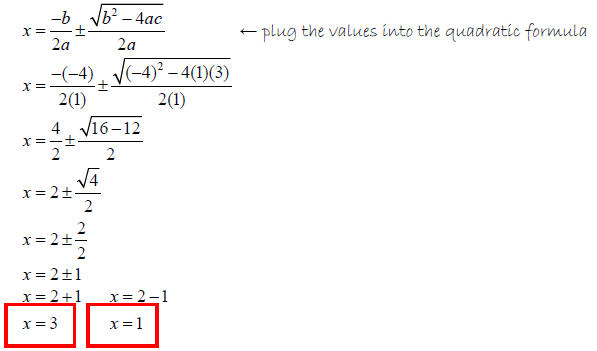
Example 4
Solve using cross- products and the quadratic formula
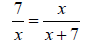
Solution

So …
a = 1; b = -7; c = -49
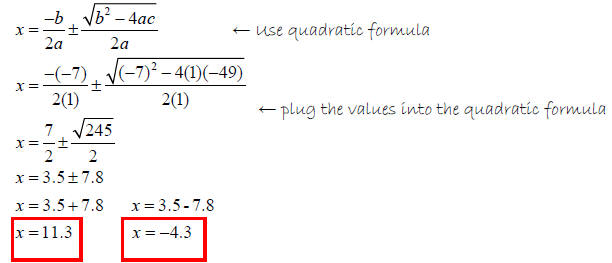
Example 5
Solve using the quadratic formula : 2(x -1)2 + 5 = 6
Solution
We must rewrite the equation in standard form…

So… a = 2, b = -4, and c = 1 ← plug these values into the quadratic formula.
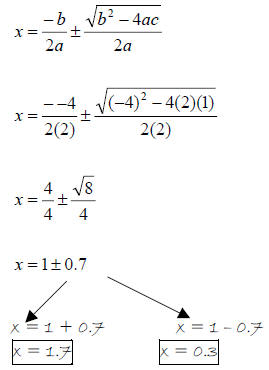
Example 6
The area of a rectangle is 25m2. The rectangle is 4m longer than it is wide.
What are the
dimensions of the rectangle?
Solution
Write an equation
Let x = width
Length = x + 4 (The rectangle is 4m longer than wide)
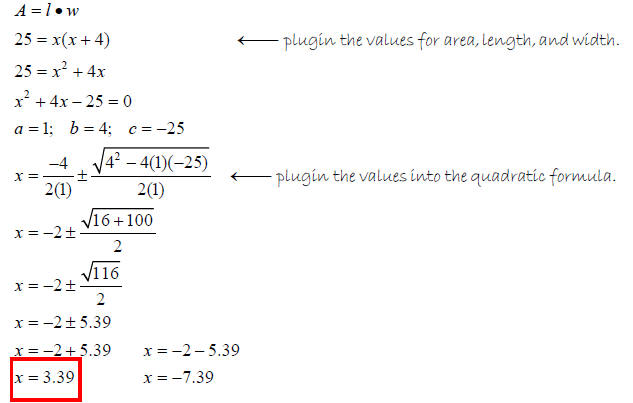
Length and width must be positive , so x = 3.39.
Warm-up
Solve each quadratic equation
1. x2 - 4x + 3 = 0
2. x2 + 5x -14 = 0
3. 2x2 + x - 3 = 0
| Prev | Next |