Linear and Quadratic Functions
Linear Functions
A linear function is a function that can be written in the
form f (x) = mx + b .
Its graph is a straight line.
m = slope
b = y-intercept
Recall: If a line passes through (x1 , y1 ) and
(x2 , y2 ) , its slope m is given by
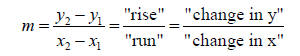
The sign of the slope indicates whether the line is an
increasing or a decreasing function.
m < 0
m > 0
Also recall:
1. The slope of any horizontal line is 0.
2. The slope of any vertical line is undefined.
Example 1: Graph the equation using its slope and
intercept:
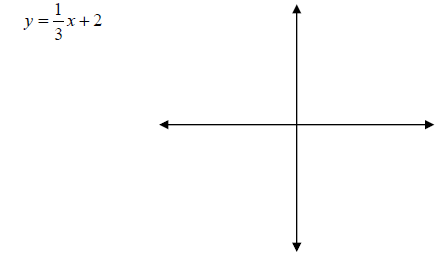
Two useful forms for the equation of a line :
1. y = mx + b (slope- intercept form )
2. y - y1 = m(x - x1 ) (point-slope form)
Note: We are working with functions, so we want y
on the left-hand side by itself.
This means we need to rearrange our equations into slope - intercept form so we
can write
f (x) = mx + b .
Parallel Lines
Two lines are parallel if they never cross. In terms of equations, two lines
are parallel if
they have __the same_____ slope.
Perpendicular Lines
Two lines are perpendicular if they meet at a right angle. In terms of
equations, two lines
with slopes m1 and m2 are perpendicular if and only if
m1* m2 = -1 .
Example 2: Find the linear function f such that f
(1) = 5 and f (2) = 8 . What is the inverse of this
function?
Example 3:Write the equation of the linear function
f(x) that passes through the point (-4,5)
and is parallel to the line 4x + 3y = 7 .
Example 4: Find the linear function f that is
perpendicular to the line containing (4,-2) and
(10,4) and passes through the midpoint of the line segment connecting these
points.
Quadratic Functions
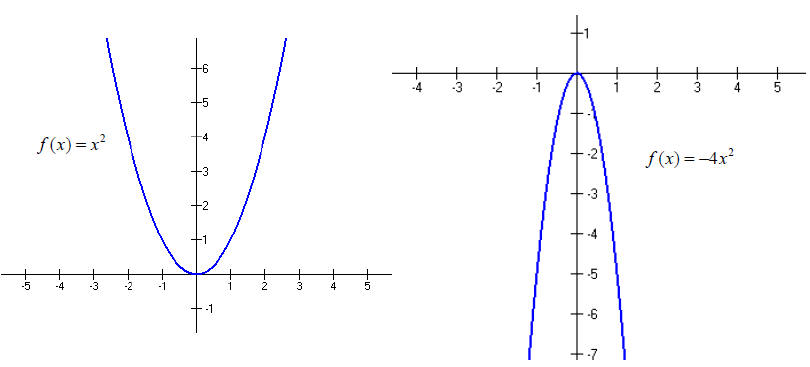
A quadratic function is a function which can be written in
the form f (x) = ax2 + bx + c
( a ≠ 0 ). Its graph is a parabola .
Every quadratic function also know as a parabola is
written as f (x) = ax2 + bx + c or can be written in
standard form: f (x) = a(x - h)2 + k . The vertex is (h, k) . The y-intercept
is f(0). The axis of symmetry is
the equation x = h.
· The graph opens up if a > 0 .
· If |a| is larger, is the parabola is narrower ; if |a| is smaller, is the parabola is wider.
a is referred to as the shape factor .
Shortcut:
For f (x) = ax2 + bx + c , the vertex is ,
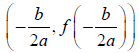 .
So the axis of symmetry is
.
So the axis of symmetry is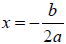 .
.You should be able to identify the following :
· Direction the graphs opens(upwards or downwards)
· Whether the function has a maximum or a minimum
· y-intercept
· coordinates of the vertex
· equations of the axis of symmetry
· maximum or minimum
Example 5: Sketch the graph of f (x) = 3x2 + 6x + 7 by finding the six features of the function.
Example 6: Sketch the graph of f (x) = -2x2 + 12x - 16 by finding the six features of the function.
Example 7: Find the quadratic function such that
the axis of symmetry is x = - 2 , the y-intercept is - 6
and there is only one x-intercept.
| Prev | Next |