Rational Numbers
Overview
• A brief introduction
• A small problem
• A few examples
• How it fits together
• Why it matters so much
• For more information
A Brief Introduction
• Taught middle school mathematics to children
considered at risk to not graduate from high
school
• Taught high school algebra to children considered
at risk to not graduate from high school
• Taught mathematics to undergraduate and
graduate students preparing to become
elementary and secondary teachers
• Taught mathematics education to graduate
students preparing to become elementary and
secondary teachers
My perspective
• Rational numbers are difficult for
students because of the way in which
the mathematics intersects with the
way people think about rational
number situations
A Small Problem ( or two )
• Think about each of the situations on
the handout. What is the meaning of ¾
in each situation?
Draw a picture to represent the
meaning of ¾ in each situation
A few examples
• New Units and Notations
1. 45 minutes of 60 minutes
in an hour, ¾ of one hour
2. 3(¼ cookies)
3. ¼(3 cookies)
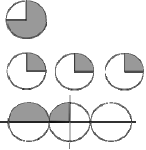
Another examples
Same notation means different things
¾ as a ratio (not part whole)
Return
And yet another example
¾ is an operator that
maps one quantity
to another
Examples I won’t
elaborate on
• Rational number as decimal
• Rational number as percent
• Rational number as rate
Fitting it all together
• Why are rational numbers hard for
children?
– In teaching, we don’t take enough time to help
students understand the meaning of rational
numbers
• The same number can mean different things,
depending on the unit
• Rational numbers often represent a relationship
between quantities, not absolute numbers
• Rational numbers require multiplicative ( not additive )
reasoning
Other kinds of
difficulties
• Notational difficulties – not everything we
write as a “fraction” is a rational number
(e.g., π/2)
• Over-reliance on part-whole metaphors for
fractions
• Interference of generalizations made
about whole numbers
• Use of “fraction” in everyday language
Why it continues to
matter
• General quantitative literacy
– “Do the math: An 11-(percentage) point
Democratic lead on the generic ballot test,
minus 5 points for the gauge's Democratic
skew, translated into a 6-point Democratic
victory. When the 6-point Democratic popular
vote win is measured against the GOP's 5-point
win in 2002 and its 3-point win in 2004, it
clearly constituted a wave.” (Cook, 2006)
• Another Interpetation
– “Wow. So in 2002, a humdrum, non-wave
election, the GOP won by 5 points. But
this year, in a "wave election that
rivaled the 1994 tsunami," the Dems won
by 6 points. See? No wave: 5. Wave: 6!”
(Kaus, 2006)
Why it matters
academically
• My previous research in
undergraduate student learning of
differential equations
– Students had difficulty with the
concept of a rate-of- change equation
because they had underlying difficulties
with the concept of rate
Conclusion
• Rational numbers are difficult for students
because of the ways in which the mathematics
intersects with the ways people think and learn
• Instruction often compounds these difficulties by
not acknowledging and making sure students have
experiences with the multiple ways to think about
rational numbers
• Weak understanding of rational numbers have long
term repercussions for students as they continue
in life and in academics
For More Information
• Lamon, S. (2006). Teaching Fractions and
Ratios for Understanding: Essential
content knowledge and instructional
strategies for teachers (2nd Edition).
Mahwah, NJ: Lawrence Erlbaum Publishers.
• The Rational Number Project
| Prev | Next |