Representations of Functions as Power Series
1. Functions we know
Recall that if x is a number with |x| < 1, then the series
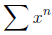
converges. In fact, since this is a geometric series with
|x| < 1, we
know that this sums to
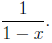
This means that provided |x| < 1, the function
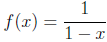
agrees with the power series
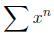
(starting from 0). By ”agrees”, we mean for any chosen
value of x
which is substituted into the equation, the infinite sum agrees with the
value of the series . This leads to two different questions:
Question 1.1. Can this power series be used to construct other power
series which are also functions?
Question 1.2. What other functions can be realized as power series?
We shall answer the second question mainly in the next section. The
first question we shall answer through a number of examples and by
utilizing tools we have developed in Calculus.
Example 1.3. For the following functions, find a power series repre-
sentation and determine the interval of convergence.

We know that
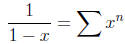
on the interval [−1, 1). Substituting − x into the
equation , we
get
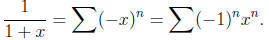
Observe that this converges on the interval (−1, 1).

We know that
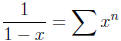
on the interval (−1, 1). Substituting −x2/9 into the
equation,
we get
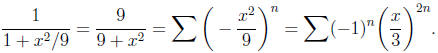
This is not quite the equation we are after , but if we
multiply
by x/9, we get
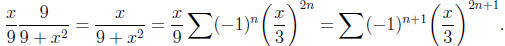
Applying the ratio test , we have
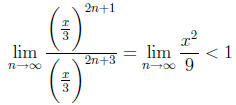
provided |x| < 3, so it converges on the interval (−3, 3).
At
the endpoint x = 3, we have
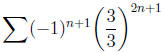
which diverges and at x = −9, we have
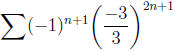
which diverges. Hence the interval of convergence is (−3, 3).
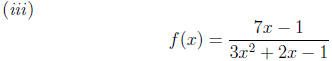
Using partial fractions , we get
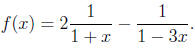
For the first, we make the substitution −x and for the second,
we make the substitution , 3x, giving
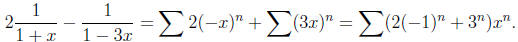
The first series converges for x in the interval (−1, 1) and the
second for (−1/3, 1/3), so the sum will converge for x in the
interval (−1/3, 1/3).
Observe that each of these functions represented as power
series were
found using simple composition of functions and other elementary alge-
braic operations . We can ask if there are other elementary operations
which can be performed on power series to obtain new ones and in par-
ticular, obtain new functions represented as power series. The following
answers this question.
Result 1.4. If the power series
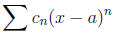
has radius of convergence R ≥ 0, then the function defined by
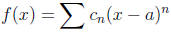
is differentiable and integrable on the interval (a − R, a + R) and
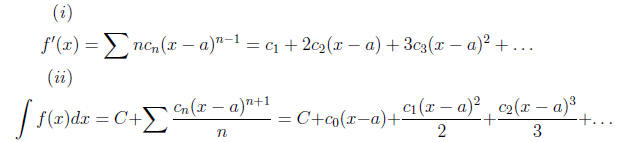
where C is some constant.
The radii of convergence are the same for both the integral and deriv-
ative, but the behavior at the endpoints may be different.
We illustrate the uses of these operations on power series with some
examples.
Example 1.5. Find power series representations for the following func-
tions and the corresponding radii of convergence.

Observe that
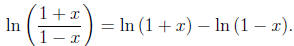
Also,
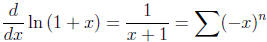
and

Thus
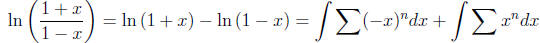
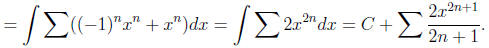
Observe that f(0) = 0, so C = 0 giving
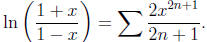
Since the radii of convergence of both of the original
series is
1, it follows that the radius of convergence of this series is 1.

Observe that
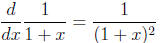
and
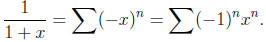
Therefore
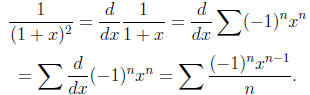
Since the radius of convergence of the original series is
1, it
follows that the radius of convergence of this series will also
be 1.
Example 1.6. Use power series to approximate the following indefinite
integral:
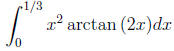
First observe that
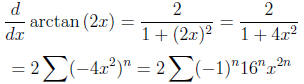
so
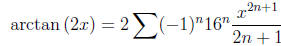
(since when x = 0 we have arctan (2x) = 0). Therefore
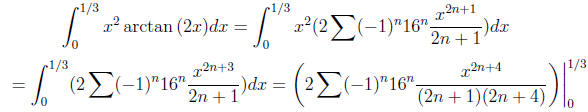
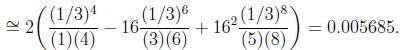
| Prev | Next |