rican Mathematics Contest 8 Solutions Pamphlet
American Mathematics Contest 8 Solutions Pamphlet
This Solutions Pamphlet gives at least one solution for
each problem on this year’s
exam and shows that all the problems can be solved using material normally
associated
with the mathematics curriculum for students in eighth grade or below. These
solutions are by no means the only ones possible, nor are they necessarily
superior
to others the reader may devise.
We hope that teachers will share these solutions with their students. However,
the
publication, reproduction, or communication of the problems or solutions of the
AMC 8 during the period when students are eligible to participate seriously
jeopardizes
the integrity of the results. Dissemination at any time via copier, telephone,
e-mail,
World Wide Web or media of any type is a violation of the competition rules .
1. (B) If multiplying a number by 2 results in 60, then
the number must be 30. If
30 is divided by 2, the correct answer is 15.
2. (C) Karl spent 5×$2.50 = $12.50 on the folders. If he had purchased the
folders
a day later, he would have saved 20% of this total, or 0.20 × $12.50 = $2.50.
OR
Karl could have bought five folders for the price of four in the 20%-off sale,
so
he could have saved $2.50.
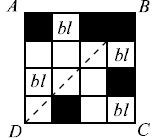
3. (D) For diagonal BD to lie on a line of symmetry in square ABCD , the four
small squares labeled bl must be colored black.
4. (C) The perimeter of the triangle is 6.1 + 8.2 + 9.7 =
24 cm. The perimeter of
the square is also 24 cm. Each side of the square is 24 ÷ 4 = 6 cm. The area of
the square is 62 = 36 square centimeters.
5. (B) To get the minimum number of packs, purchase as many 24-packs as pos-
sible. three 24-packs contain 72 cans, which leaves 90 - 72 = 18 cans. To get
the remaining 18 cans, purchase one 12-pack and one 6-pack. The minimum
number of packs is 5.
6. (C) The number 2.00d5 is greater than 2.005 for d = 5, 6, 7, 8 and 9.
Therefore,
there are five digits satisfying the inequality .
7. (B) The diagram on the left shows the path of Bill's
walk. As the diagram on
the right illustrates, he could also have walked from A to B by first walking 1
mile south then 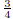 mile east.
mile east.
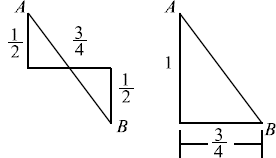
By the Pythagorean Theorem,
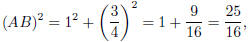
so 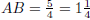 .
.
8. (E)
To check the possible answers, choose the easiest odd numbers for m and n. If
m = n = 1, then
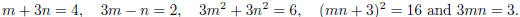
This shows that (A), (B), (C) and (D) can be even when m and n are odd.
On the other hand, because the product of odd integers is always odd, 3mn is
always odd if m and n are odd.
Questions. Which of the expressions are always even if m and n are odd? What
are the possibilities if m and n are both even? If one is even and the other
odd?
9. (D) Triangle ACD is an isosceles triangle with a 60± angle, so it is also
equi-
lateral. Therefore, the length of 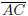 is 17.
is 17.
10. (D) Covering the same distance three times as fast takes one-third the time.
So
Joe ran for 2 minutes. His total time was 6 + 2 = 8 minutes.
11. (C) To add 6% sales tax to an item, multiply the price by 1.06. To calculate
a
20% discount, multiply the price by 0.8. Because both actions require only mul-
tiplication, and because multiplication is commutative, the order of operations
doesn't matter. Jack and Jill will get the same total.
Note. Jack's final computation is 0.80(1.06 × $90.00) and Jill's is 1.06(0.80 ×
$90.00). Both yield the same product , $76.32.
12. (D) You can solve this problem by guessing and
checking. If Big Al had eaten
10 bananas on May 1, then he would have eaten 10 + 16 + 22 + 28 + 34 = 110
bananas. This is 10 bananas too many, so he actually ate 2 fewer bananas each
day. Thus, Big Al ate 8 bananas on May 1 and 32 bananas on May 5.
OR
The average number of bananas eaten per day was
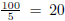 . Because the
. Because the
number of bananas eaten on consecutive days differs by 6 and there are an odd
number of days, the average is also the median. Therefore, the average number
of bananas he ate per day, 20, is equal to the number of bananas he ate on May
3. So on May 5 Big Al ate 20 + 12 = 32 bananas.
OR
Let x be the number of bananas that Big Al ate on May 5. The following chart
documents his banana intake for the five days.
| May 5 | May 4 | May 3 | May 2 | May 1 |
| x | x - 6 | x - 12 | x - 18 | x - 24 |
The total number of bananas Big Al ate was 5x - 60, which
must be 100. So
Big Al ate 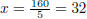 bananas on May 5.
bananas on May 5.
| Prev | Next |