Scientific Notation

A number with an exponent implies repeated multiplication by the value of the exponent. Thus
10² = 10 × 10 = 100, 10³ = 10 × 10 × 10 = 1,000, etc.

Using this idea as a basis, we can think of the action of a positive exponent of 10 as shifting the
decimal point to the right starting with 1. Thus, 10² can be thought of as mechanically shifting the
decimal point to the right by 2 places starting from the value 1, which has an implied decimal
point just after the digit (and adding 0s as needed as we go). This method becomes more and
more advantageous as the magnitude of the number increases. For example, 10⁹, which would
correspond to 1,000,000,000 is just as easy to write as 10², even though the value is much greater
and the standard decimal representation is much longer.

If positive exponents can be thought of as shifting the decimal point to the right, then we can
extend the idea by saying that negative exponents imply a shifting of the decimal point to the left.
As above, we add 0s as we do this, except that now the 0s are in front of the 1 rather than after it.
Thus 10^-2 means 1 with the decimal point shifted left by 2 places, or 0.01, and 10^-3 means 1 with a
decimal point shifted to the left 3 places, or 0.001. Just as for positive exponents, which are a
convenient way of expressing very large numbers, negative exponents are very convenient for
expressing very small numbers. Thus, 10^-9 = 0.000 000 001.

In some cases it is not possible to deal with superscript exponents for typographical reasons. In
these cases we can use an entirely equivalent notation using the letter e. Thus 1e+2 and 1e-3 are
completely equivalent to10² and 10^-3, respectively.

Using this method, we can express any number as a product of a relatively small value and an
appropriate power of 10. Thus, 200 = 2 × 100 = 2 × 10² = 2e+2, and 25,000 = 25 × 1,000 = 25 ×
10³ = 25e+3. We can use the same ideas for very small numbers. Thus 0.005 = 5 × 10^-3 = 5e-3.
There is always more than one way of expressing a number in scientific notation, and the one that
we choose is purely a matter of convenience. Thus, 25,000 = 2.5e+4 = 25e+3 = 250e+2 =
2500e+1. As you can see, the value need not be an exact integer – the method works in just the
same way whether the value is 2.5 or 25.

In addition to making it easy to represent very small and very large values, scientific notation can
simplify multiplication and division. We can show the rules for multiplication by comparing the
same calculation expressed using integer and scientific notations. For example, consider

500 × 20 = 10,000

which we could express in scientific notation as

5e+2 × 2e+1 = 10e+3

Using this example as a template, the rule for multiplying numbers in scientific notation is: First,
multiply the two integers to compute the integer of the answer, and then add the two exponents to
get the exponent of the answer. We would have gotten the same answer if we had chosen another
way of expressing the values in scientific notation. For example, we could have used the
equivalent expression :

0.5e+3 × 2e+1 = 1e+4

To see how to divide two numbers in scientific notation, consider the example

4000/50 = 80

which we could express in scientific notation as

40e+2/5e+1 = 8e+1

Using this example as a template, the rule for dividing numbers in scientific notation is: First,
divide the two integers to compute the integer of the answer, and then subtract the two exponents
to get the exponent of the answer.

Finally, consider the division of a number by itself:

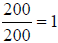
Using scientific notation and our division rule, this would be written as:

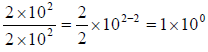
This result shows that 10⁰ = 1. This should not seem unreasonable. If a positive exponent is an
indicator to shift the decimal point to the right starting from 1, and if a negative exponent is an
indicator to shift the decimal to the left starting from 1, then an exponent of 0 should mean to
leave the decimal point alone, so that the value would be unchanged.

There is usually no advantage in using scientific notation for addition and subtraction except in
the special case when we are adding and subtracting numbers that have the same exponent. In this
special case, we simply add or subtract the numbers and use the common exponent for the
exponent of the answer. Thus,

500 + 200 = 700

or, in scientific notation,

5×10² + 2×10² = 7×10²

and

800 – 500 = 300

or, in scientific notation,

8×10² - 5×10² = 3×10²

If the two numbers we are adding or subtracting do not have the same exponent initially, it may
be possible to convert one of them to another equivalent form. Thus,

500 + 20 = 520

could not be handled as

5×10² + 2×10¹

since the exponents are not the same. However, we could add them using the form

50×10¹ + 2×10¹ = 52×10¹

which gives the same answer as using the integers.