SOLUTIONS FOR HOMEWORK 6: NUMBER THEORY
6. (a) Show that if n > 1 is composite, then there exists
d in the range 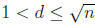 such
such
that d|n. (Hint: you might want to use proof by contradiction).
Proof by contradiction. Suppose for all d in the range
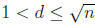 does not divide
does not divide
n. In other words, all divisors of n greater than 1 are in fact greater than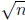 .
Since n is
.
Since n is
composite, there exists an integer e in the range 1 < e < n such that e|n. Then
ef = n for
some integer f. Since f is also a positive divisor of n, it follows from our
assumption that
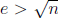 and
and 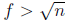 .
(Note that we cannot have f = 1 because e < n and we cannot have
.
(Note that we cannot have f = 1 because e < n and we cannot have
f = n because e > 1). But then 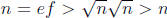 is a
contradiction. Thus, if n > 1 is
is a
contradiction. Thus, if n > 1 is
composite, it must admit a divisor in the range
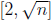 .
.
(b) Use (a) to show that if n > 1 is not divisible by any integers in the range
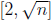 , then
, then
n is prime.
Suppose n > 1 is not divisible by any integers in the range
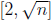 . If n were composite,
. If n were composite,
then by (a), it would have a divisor in this range, so n must be prime.
(c) Use (b) to show that if n is not divisible by any primes in the range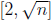 ,
then n
,
then n
is prime.
Proof by contradiction. Suppose n > 1 is not divisible by any primes in the
range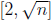 .
.
and that n is composite. By (a), n is divisible by some integer
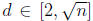 . Since every
. Since every
integer > 1 is divisible by at least one prime , there exists a prime p|d, so of
course p|n
since d|n. Since 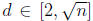 and 2 ≤ p ≤d, we have
and 2 ≤ p ≤d, we have 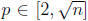 is prime and divides n, a
is prime and divides n, a
contradiction. This completes the proof.
(d) Use the procedure in (c) to verify that 229 is prime.
We check that 229/p for p = 2, 3, 5, 7, 11, 13 gives non- zero remainder . Since
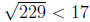 ,
,
we are done by (c).
(e) Suppose you write down all the primes from 2 to n. We know that 2 is a prime
so we
circle it and cross out all other multiples of 2. The next uncrossed number is 3
and we claim
that 3 therefore must be prime. Explain why. Now cross out all the multiples of
3. The next
uncrossed number is 5 so we claim it must be a prime. We continue in this
fashion until we
get to ![]() . Explain why
all the remaining numbers are prime. Carry out this procedure for
. Explain why
all the remaining numbers are prime. Carry out this procedure for
n = 100 to find all the primes less than 100. This is called the Eratosthenes
sieve. (You may
want to write them in 10 rows of 10 numbers each).
Once we cross out multiples of 2, 3, . . . , 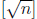 ,
any number that remains does not have a
,
any number that remains does not have a
divisor less than or equal to
![]() so must be prime by
(c).
so must be prime by
(c).
7. (a) Prove that if n ∈ N, then gcd(n, n + 1) = 1.
Suppose d|n and d|(n + 1). Then d|(n + 1 − n) by Problem 1, i.e. d|1 so d = ±1.
Thus,
gcd(n, n + 1) = 1.
(b) Is it possible to choose 51 integers in the interval [1, 100] such that no
two chosen
numbers are relatively prime? [i.e. is there a subset
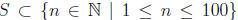 with
with
|S| = 51 such that m, n ∈ S ) => gcd(m, n) > 1?] Prove that your answer is
correct. (Hint:
If you get stuck, recall that an often useful problem- solving strategy is to
attempt a simpler
problem first, so think about 6 integers in [1, 10] for example).
Suppose 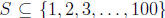 and |S| = 51. I claim there exists 1
≤n ≤99 such that
and |S| = 51. I claim there exists 1
≤n ≤99 such that
n∈ S and n + 1 ∈ S. We can prove this claim by contradiction. Suppose not. Then
if we
list the elements of S in increasing order as 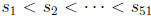 , we have
, we have 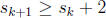 for
for
1 ≤ k ≤50. Thus, 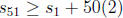 . Since
. Since
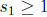 , it follows that
, it follows that
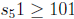 a contradiction.
a contradiction.
Thus, there exists 1 ≤n ≤99 such that n, n + 1 ∈ S. Then gcd(n, n + 1) = 1 by a
previous
problem. So we cannot have a subset of size 51 in {1, 2, 3, . . . , 100} no two
of whose elements
are relatively prime.
8. Show that for n ≥1, in any set of 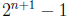 integers, there is a subset of exactly
integers, there is a subset of exactly 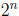 of
of
them whose sum is divisible by 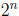 . (Hint: use
ordinary induction on n).
. (Hint: use
ordinary induction on n).
To ease the notation, let us make a definition. If S is a finite subset of Z,
let us define
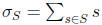 to be the sum of its elements. We want to
prove, for n ≥1,
to be the sum of its elements. We want to
prove, for n ≥1,
P(n) : If 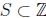 has size
has size
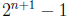 , then there exists
, then there exists
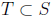 of size
of size 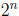 such that
such that
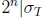 .
.
Induction on n. Base case n = 1. Given 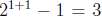 integers, say a, b, c, at least 2 of
integers, say a, b, c, at least 2 of
them must have the same parity, by the pigeonhole principle (there are only two
possible
“parity pigeonholes” namely even and odd, so the three “pigeons” (a, b, c)
cannot get three
distinct pigeonholes). So, we take two that have the same parity: their sum is
even, i.e. is
divisible by 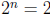 . This takes care of the base
case.
. This takes care of the base
case.
Induction step. Suppose k ≥1 is some integer such that the proposition is true
for all
subsets of Z of size 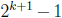 . Suppose
. Suppose
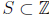 and
and
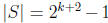 . We are looking for a subset
. We are looking for a subset
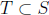 of size
of size 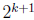 such that
such that
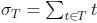 is divisible by
is divisible by
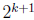 .
.
Step 1. Chop Shop. If we set aside a random element, say x ∈ S, we
can chop up the
rest of S into two subsets 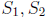 of equal size,
i.e.
of equal size,
i.e.
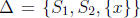 is a partition where
is a partition where
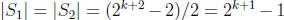 . There are many choices for
. There are many choices for
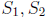 , x of course, we just
, x of course, we just
choose any one we like .
Step 2. A tale of two pigeons. By the induction hypothesis, there exist
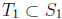 and
and
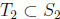 of size
of size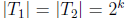 such that
such that
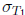 and
and 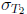 are
divisible by
are
divisible by
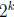 . It is tempting to
. It is tempting to
take 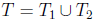 , but then we will have only that
, but then we will have only that
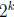 divides T . Namely we have
divides T . Namely we have 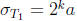
and 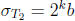 so
so 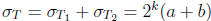 .
So what is the problem? The problem is that
.
So what is the problem? The problem is that
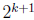 divides
divides 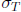 if and only if 2|(a+b), i.e. if and only if a, b have the same parity. Now,
since
if and only if 2|(a+b), i.e. if and only if a, b have the same parity. Now,
since
we have only two numbers, a, b, we can’t guarantee they have the same parity!
(conclusion:
not enough pigeons!) Got to get me some more pigeons by golly.
Step 3. The magical third pigeon. The critical step in this problem is to
realize that
if we could find another “pigeon” i.e. another subset
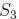 of S of size
of S of size
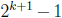 , then inside it we
, then inside it we
can find 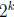 elements that add up to something
of the form
elements that add up to something
of the form
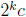 with c ∈ Z, then among a, b, c
with c ∈ Z, then among a, b, c
we’ll be able to find two of the same parity. BUT, we have already used up the
elements of
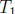 and
and 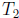 and
do not want to disturb them, so we have to make sure that
and
do not want to disturb them, so we have to make sure that
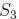 is disjoint from
is disjoint from
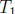 and
and 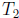 (i.e. we don’t have any “interference” when we add up the sums). If you think
(i.e. we don’t have any “interference” when we add up the sums). If you think
about this, then you eventually have the brilliant idea that maybe we should
count up how
many elements are left outside 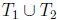 to see if we
have enough elements left. Well,
to see if we
have enough elements left. Well,
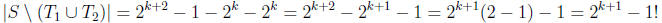
That last “!” is a “surprise” not a “ factorial ,” by the
way. In other words, if we gather
together all the elements we have not yet used up, they form a subset
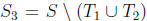
of size 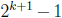 , so we can apply the induction step
once again to find a subset
, so we can apply the induction step
once again to find a subset
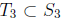 of
of
size 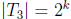 such that
such that 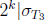 . Now, by construction,
. Now, by construction,
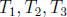 are pairwise disjoint. Now,
are pairwise disjoint. Now,
among the three numbers 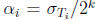 , for i = 1, 2, 3, by
the base case, we are guaranteed
, for i = 1, 2, 3, by
the base case, we are guaranteed
two of them add up to an even number, say  is
even. Then taking
is
even. Then taking 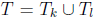 , we
, we
have 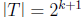 and
and 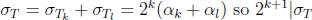 .
.
9. Suppose x is a real number such that x+1/x is an integer. Show that
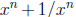 is also
is also
an integer for all n ≥1. (Hint: Use complete induction on n).
To ease the notation, let us put α = (x + 1/x) ∈ Z and, for
n ≥1,
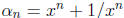 . The
. The
proposition is clearly true for n = 1 since 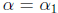 .
Let us do n = 2 to see what is involved.
.
Let us do n = 2 to see what is involved.
We have 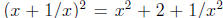 , so
, so
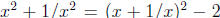 . Thus, if ∈ Z, then
. Thus, if ∈ Z, then
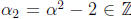 since
since 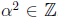 .
So there should be some nice relationship between
.
So there should be some nice relationship between
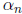 and
and
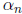 . Rather, there is a neater relationship
between
. Rather, there is a neater relationship
between
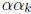 and
and 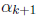 .
.
Well, let us go to the induction step. We assume, for some integer k ≥1, that 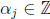 for
for
1 ≤ j ≤ k. We compute
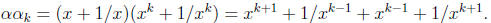
In other words,
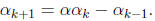
By the (complete) induction step, we know that
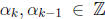 , and certainly
, and certainly
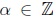 so
so
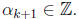
By the principle of complete mathematical induction , we are done.
10. Here is a “proof” by complete induction that all Fibonacci numbers are even!
Your
job is to explain the error in the argument.
For n ≥ 0, let P(n) be the statement that
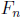 is even. We will prove P(n) by complete
is even. We will prove P(n) by complete
induction on n. We check the base case, 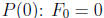 is even. Now we move to the induction
is even. Now we move to the induction
step: We must show that if P(j) holds for 0 ≤ j ≤ n, then P(n) holds. Well, if
P(j) holds
for 0 ≤ j ≤ n, then 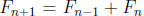 is even because
is even because
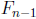 and
and
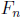 are even by P(n − 1)
are even by P(n − 1)
and P(n), respectively. By Complete Induction, therefore,
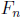 is even for all n ≥ 0.
is even for all n ≥ 0.
The error is in the step where P(n − 1) and P(n) are both used. For n = 1, this
requires
both P(0) and P(1) to be true. So, when one wants to do the base case, one needs
to check
both P(0) and P(1). It is not enough to check P(0). Indeed, when one tries to
check P(1),
it turns out to be false, for 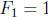 is odd.
is odd.
| Prev | Next |