Solving Linear Equations

1.5 Solving Linear Equations
In this section we study various methods, algebraic and graphical , for solving
equations of the form

f(x) = g(x) (1)

where both f(x) and g(x) are linear functions .
To solve Equation (1) algebraically, isolate the variable on one side of the
equation (traditionally, the left side). This can be done thanks to the follow-
ing two properties of numbers .

Property I. Adding or subtracting the same number to both sides of an
equation does not change the solution to the equation.
Property II. Multiplying or dividing both sides of an equation by a nonzero
number does not change the solution to the equation.

Remark 1
The above two properties apply to any equation and not only for linear
equations.

Example 1
Solve the equation 1 - 2(3 - x) = 10 + 5x.

Solution.
Multiplying we find 1-6+2x = 10+5x or 2x-5 = 10+5x. Add -2x-10
to both sides to obtain 3x = -15. Divide both sides by 3 to obtain x = -5.

If Equation (1) involves fractions, it is usually recommended to remove the
denominators by multiplying both sides of the equation by the least common
denominator.

Example 2
Solve.

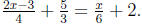
Solution.
Multiply through by the least common denominator 12 to obtain 3(2x-3)+
4(5) = 2x+2(12). This can be rewritten as 6x+11 = 2x+24. Add -2x-11
to both sides to obtain 4x = 13. Divide both sides by 4 to otbtain x = 13/4

Now, Equation(1) can be solved geometrically. Indeed, since both f(x) and
g(x) are linear functiones their graphs are straight lines. So we can enter
each function into a graphing calculator and graph to obtain two lines. If
the two lines are parallel then we say that Equation (1) has no solutions. If
the window shows only one line then we say that the equation has an infinite
number of solutions. If the window shows two intersecting lines then the
equation has a unique solution. This unique solution can be found by using
the key INTERSECT found in your calculator. (For the TI-83, this found
by pressing 2nd and CALC).

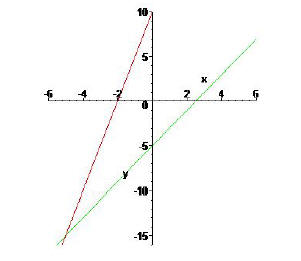
Example 3
Solve graohically the equation 1 - 2(3 - x) = 10 + 5x.

Solution.
Geometrically, the point (-5;-15) is the point of intersection of the two
lines f(x) = 1-2(3-x) = 2x-5 and g(x) = 10+5x as shown in the figure
below

Solving Literal Equations
By a literal equation we mean an equation involving many letters. For ex-
ample, in finance, an investment of P dollars for t years at a simple interest
rate of r grows to a balance given by the formula A = P(1 + rt).

Example 4
Solve the equation A = P(1 + rt) for t.

Solution.
Distributing on the right we find A = P + Prt. Subtract P from both sides
to obtain Prt = A - P. Now, divide both sides by Pr to obtain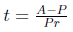
We conclude this section with an application problem

Example 5
The value of a new computer equipment is $20,000 and the value drops at a
constant rate so that it is worth $ 0 after five years. Let V (t) be the value
of the computer equipment t years after the equipment is purchased.

(a) Find the slope m and the vertical intercept b.
(b) Find a formula for V (t).
(c) How long does it take for the computer's value to depreciate to $4000?

Solution.
(a) Since V (0) = 20; 000 and V (5) = 0 then the slope of V (t) is

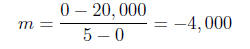
and the vertical intercept is V (0) = 20; 000.
(b) A formula of V (t) is V (t) = -4; 000t + 20; 000.
(c) We must find t so that V (t) = 4000 or 20; 000 - 4; 000t = 4000. This
implies 4000t = 16; 000 or t = 4 years