Some Irrational Numbers
Who found the first irrational?
| ● The first irrational number, sqrt(2), is commonly credited to the Pythagoreans, and in particular to Hippasus. The Pythagoreans were strong believers that all numbers could be expressed by integers, or their ratios. It was also unpleasant to hold ideas that didn't fit into this mold. |
 |
Hippasus's Fate
| Hippasus was so excited at his new finding, that he went off to enjoy his favorite activity, diving off a plank into shark infested waters wearing nothing but the finest cuts of meat. |
 |
Irrational Numbers
● What's an Irrational number?
● An Irrational number is not rational, and a
rational number is representable as a reduced
fraction .
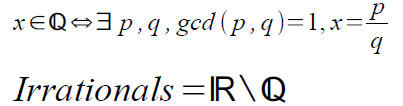
●Rationals can also be said to be the set of numbers which
solve
● a linear polynomial with coefficients in Z .
Some properties?
● Not representable as a terminating or repeating decimal .
● Do we have closure under addition or multiplication ?
● Are they bigger than the set of rational numbers? (Anyone know a 1-1 map from
irrationals to reals?)
Closure?
● No sir, we've got no closure.
● Addition?
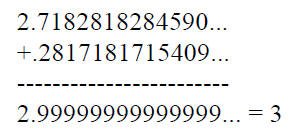
●Multiplication?
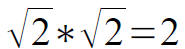
●Anti-Closed? Adding or multiplying by a rational will give an Irrational.
How big are they?
● The rational numbers are big, but can be put into
a 1-1 correspondence with the integers, so we call
them countable.
● The real numbers are uncountable (Cantor's
diagonal argument), so the stuff left over after
we've taken out a countable set must be
uncountable, in this case that's the irrationals.
Everyone's favorite unspeakable proof
● To get things started, let's show the irrationality
of a simple number. Assume sqrt(2) is rational
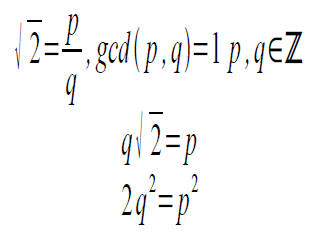 |
Now we take the prime factorization of each side. The power of 2 on the left hand side must be odd, and it is even on the right hand side. This is no good so perhaps we were a bit batty in assuming that sqrt(2) was rational, and it is irrational. |
But Daddy! I wanted more irrationals!
● So we've gone and shown that one number is
irrational, and the proof works for the square root
of any prime number, such as 7, 13 or 31511.
● We can also get more by adding and multiplying
rationals to any previously found irrational
number.
● But that's not enough!
Some more irrational proofs
● Let's see how far we can go by contradiction.
Now we go after a trickier number, e.
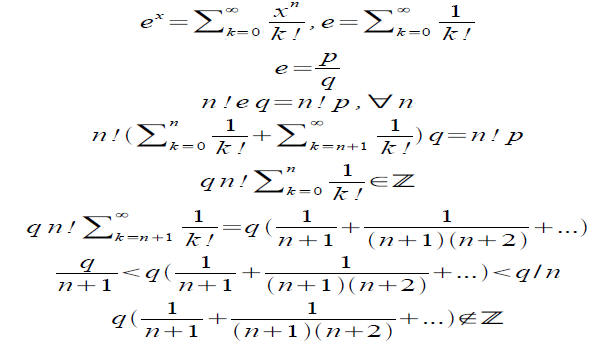
The left overs are slightly bigger than 0, and smaller than 1.
E Squared?
● Can we user the same sort of trick to show e^2 is irrational? Almost...
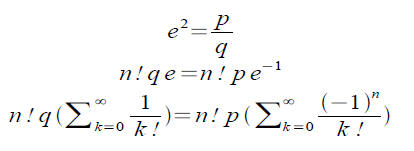
We showed last slide that the left hand side is slightly
larger than an integer, maybe we can show the right
hand side is slightly smaller than an integer.
The right hand side
● Now we play with the right hand side.
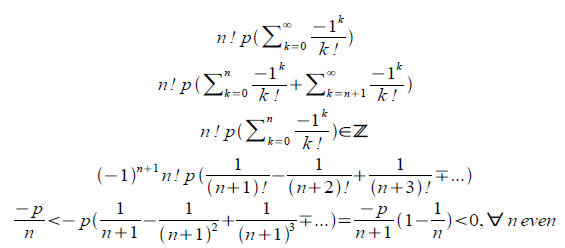
So we've found out that the right hand side is just a bit smaller
than an integer, but the left hand side was a tiny bit bigger than
an integer. Surely this can't be! So now we've found that e^2
is also an irrational number.
Bigger Powers?
We will have to change our strategy for e^4. What happens if we multiply by n!?
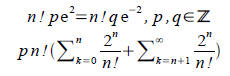
The second summand, the non integer part now goes to something like
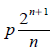
This doesn't get smaller as n goes to infinity, can we get rid of the extra powers of 2?
Get rid of that power of 2!
Suppose n is a power of 2, then how many powers of 2 are there in n!?
| n/2 | (even numbers) |
| +n/4 | (numbers divisible by 4) |
| + n/8 | (numbers divisible by 8) |
| + .... | |
| -------- | |
| n-1 |
Using similar reasoning, we can see any other
factorial will have few factors of 2 in it. With
this in mind, we have another idea of what to
multiply by. Here n is a power of 2.
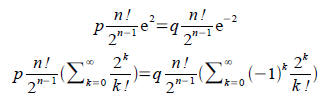
The first n tems in the sum look like
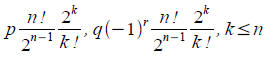
This is an integer since k! has at most k-1 powers of 2. Since n was even
the remainder is
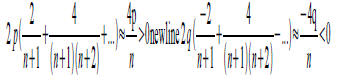
Since the left hand side of the equation is an arbitrarily small amount
larger than an integer, and the right is an arbitrarily small amount
smaller than an integer, we've found a contradiction
Such a scheme works for showing numbers of the form e2p are
irrational numbers. If we use some fancier machinery, we can show
er is irrational, for r a rational number. First we look at a particular
polynomial which will be of use.
Nifty polynomial
● Let's look at the following polynomial
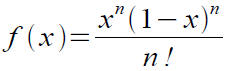
What else can we say about this polynomial? First it also has the form
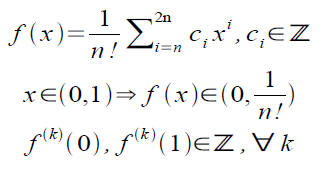
The first 2 statements are easily seen, but the third is a bit trickier.
Statement 3?
● The last bit?
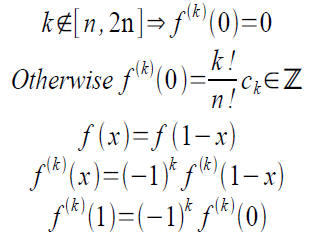
Put this polynomial to work
● So we've got a polynomial with some nice
properties, so let's try and show that er, for a
rational r must be irrational. It is enough to show
ep is irrational for an integer p. Assume es is
rational
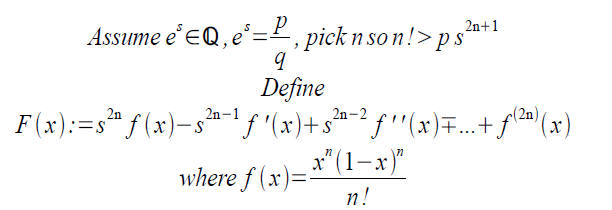
Proof (cont)
● Make it an infinite sum (the rest of the terms are 0)
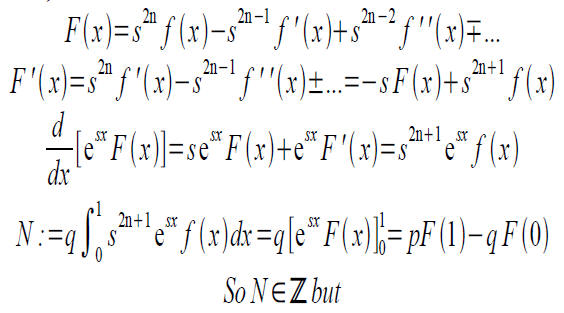
Bounding?
● We also have a bound for the integral from our
second result in the lemma.
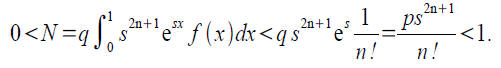
Since there aren't any integers between 0 and 1, so es is not rational.
Again, Again!
That seemed nice, let's try again with π^2.
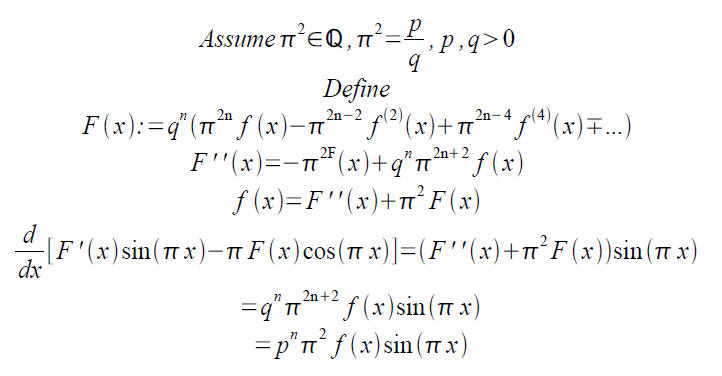
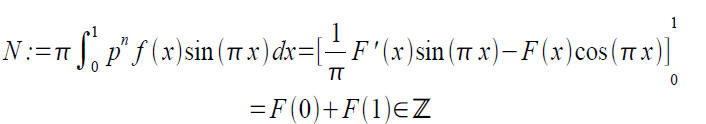
So N is a positive integer (the integrand is positive), but...
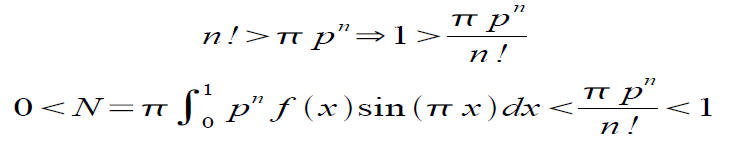
But this can't be. We've found our contradiction
And now for something completely diffrent
● Here is one more set of irrational numbers, with a different proof .
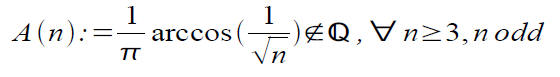
This is equivalent to saying that if we start at a point
on the unit circle and pick an orientation, and begin
circling around with chords of length 1 / √n, then we
will never hit a point twice.
A helpful trig identity
We will make use of the following trig identity, to get a
recursion
formula.
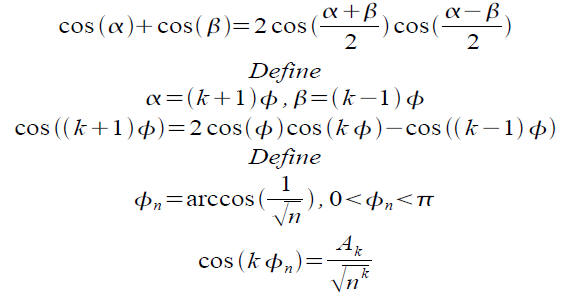
Churn, churn
By induction we have
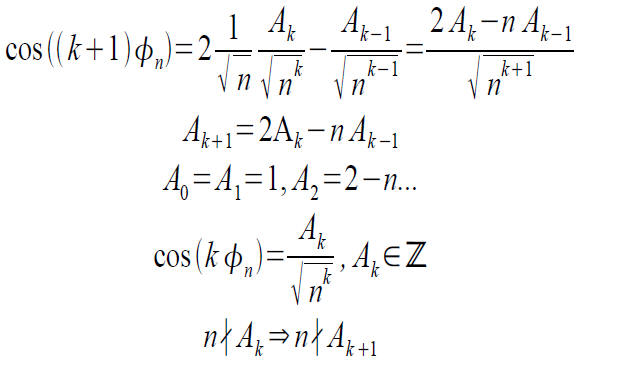
To the contradiction!
Assume that we do have a rational number
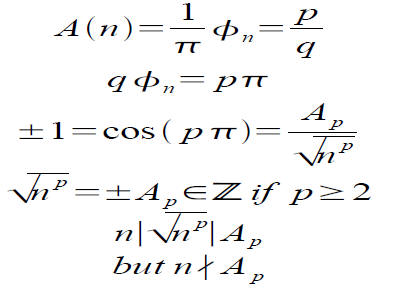
Fin!
● Prizes (Irrational -> Real 1-1 Map?,
Transcendental -> Real 1-1 Map?)
● Thanks to Erdös, and the “Proofs from the Book”
| Prev | Next |