SOLUTIONS FOR HOMEWORK 6: NUMBER THEORY

6. (a) Show that if n > 1 is composite, then there exists d in the range 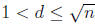such
that d|n. (Hint: you might want to use proof by contradiction).

Proof by contradiction. Suppose for all d in the range 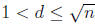does not divide
n. In other words, all divisors of n greater than 1 are in fact greater than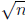. Since n is
composite, there exists an integer e in the range 1 < e < n such that e|n. Then ef = n for
some integer f. Since f is also a positive divisor of n, it follows from our assumption that
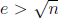and 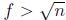. (Note that we cannot have f = 1 because e < n and we cannot have
f = n because e > 1). But then 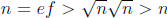is a contradiction. Thus, if n > 1 is
composite, it must admit a divisor in the range .

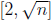(b) Use (a) to show that if n > 1 is not divisible by any integers in the range 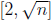, then
n is prime.

Suppose n > 1 is not divisible by any integers in the range 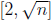. If n were composite,
then by (a), it would have a divisor in this range, so n must be prime.

(c) Use (b) to show that if n is not divisible by any primes in the range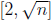, then n
is prime.

Proof by contradiction. Suppose n > 1 is not divisible by any primes in the range.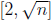
and that n is composite. By (a), n is divisible by some integer 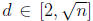. Since every
integer > 1 is divisible by at least one prime , there exists a prime p|d, so of course p|n
since d|n. Since 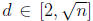and 2 ≤ p ≤d, we have 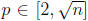is prime and divides n, a
contradiction. This completes the proof.

(d) Use the procedure in (c) to verify that 229 is prime.

We check that 229/p for p = 2, 3, 5, 7, 11, 13 gives non- zero remainder . Since ,
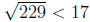we are done by (c).

(e) Suppose you write down all the primes from 2 to n. We know that 2 is a prime so we
circle it and cross out all other multiples of 2. The next uncrossed number is 3 and we claim
that 3 therefore must be prime. Explain why. Now cross out all the multiples of 3. The next
uncrossed number is 5 so we claim it must be a prime. We continue in this fashion until we
get to . Explain why all the remaining numbers are prime. Carry out this procedure for
n = 100 to find all the primes less than 100. This is called the Eratosthenes sieve. (You may
want to write them in 10 rows of 10 numbers each).

Once we cross out multiples of 2, 3, . . . , 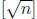, any number that remains does not have a
divisor less than or equal to so must be prime by (c).

7. (a) Prove that if n ∈ N, then gcd(n, n + 1) = 1.

Suppose d|n and d|(n + 1). Then d|(n + 1 − n) by Problem 1, i.e. d|1 so d = ±1. Thus,
gcd(n, n + 1) = 1.

(b) Is it possible to choose 51 integers in the interval [1, 100] such that no two chosen
numbers are relatively prime? [i.e. is there a subset 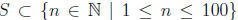with
|S| = 51 such that m, n ∈ S ) => gcd(m, n) > 1?] Prove that your answer is correct. (Hint:
If you get stuck, recall that an often useful problem- solving strategy is to attempt a simpler
problem first, so think about 6 integers in [1, 10] for example).

Suppose 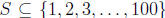and |S| = 51. I claim there exists 1 ≤n ≤99 such that
n∈ S and n + 1 ∈ S. We can prove this claim by contradiction. Suppose not. Then if we
list the elements of S in increasing order as 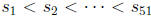, we have 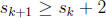for
1 ≤ k ≤50. Thus, 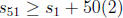. Since 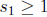, it follows that 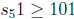a contradiction.
Thus, there exists 1 ≤n ≤99 such that n, n + 1 ∈ S. Then gcd(n, n + 1) = 1 by a previous
problem. So we cannot have a subset of size 51 in {1, 2, 3, . . . , 100} no two of whose elements
are relatively prime.

8. Show that for n ≥1, in any set of 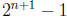integers, there is a subset of exactly 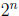of
them whose sum is divisible by 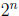. (Hint: use ordinary induction on n).

To ease the notation, let us make a definition. If S is a finite subset of Z, let us define
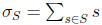to be the sum of its elements. We want to prove, for n ≥1,

P(n) : If 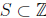has size 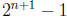, then there exists 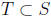of size 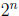such that .

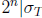Induction on n. Base case n = 1. Given 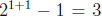integers, say a, b, c, at least 2 of
them must have the same parity, by the pigeonhole principle (there are only two possible
“parity pigeonholes” namely even and odd, so the three “pigeons” (a, b, c) cannot get three
distinct pigeonholes). So, we take two that have the same parity: their sum is even, i.e. is
divisible by 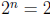. This takes care of the base case.

Induction step. Suppose k ≥1 is some integer such that the proposition is true for all
subsets of Z of size 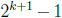. Suppose 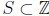and 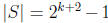. We are looking for a subset
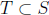of size 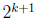such that 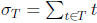  is divisible by .

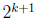Step 1. Chop Shop. If we set aside a random element, say x ∈ S, we can chop up the
rest of S into two subsets 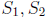of equal size, i.e. 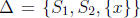is a partition where
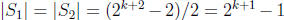. There are many choices for 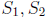, x of course, we just
choose any one we like .

Step 2. A tale of two pigeons. By the induction hypothesis, there exist 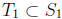and
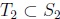of size 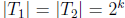such that 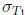and 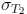are divisible by 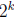. It is tempting to
take 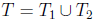, but then we will have only that 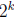divides T . Namely we have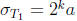
and 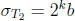so 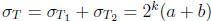. So what is the problem? The problem is that
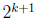divides 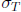if and only if 2|(a+b), i.e. if and only if a, b have the same parity. Now, since
we have only two numbers, a, b, we can’t guarantee they have the same parity! (conclusion:
not enough pigeons!) Got to get me some more pigeons by golly.

Step 3. The magical third pigeon. The critical step in this problem is to realize that
if we could find another “pigeon” i.e. another subset 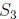of S of size 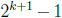, then inside it we
can find 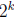elements that add up to something of the form 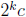with c ∈ Z, then among a, b, c
we’ll be able to find two of the same parity. BUT, we have already used up the elements of
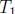and 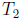and do not want to disturb them, so we have to make sure that 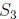is disjoint from
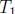and 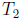(i.e. we don’t have any “interference” when we add up the sums). If you think
about this, then you eventually have the brilliant idea that maybe we should count up how
many elements are left outside 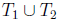to see if we have enough elements left. Well,

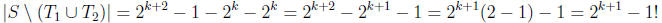
That last “!” is a “surprise” not a “ factorial ,” by the way. In other words, if we gather
together all the elements we have not yet used up, they form a subset
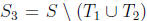
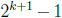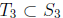of size , so we can apply the induction step once again to find a subset of
size 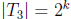such that 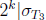. Now, by construction, 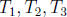are pairwise disjoint. Now,
among the three numbers 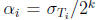, for i = 1, 2, 3, by the base case, we are guaranteed
two of them add up to an even number, say 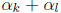is even. Then taking 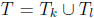, we
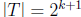have and .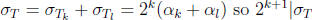

9. Suppose x is a real number such that x+1/x is an integer. Show that 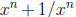is also
an integer for all n ≥1. (Hint: Use complete induction on n).

To ease the notation, let us put α = (x + 1/x) ∈ Z and, for n ≥1, 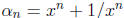. The
proposition is clearly true for n = 1 since 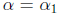. Let us do n = 2 to see what is involved.
We have 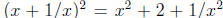, so 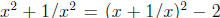. Thus, if ∈ Z, then
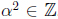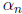since . So there should be some nice relationship between and
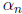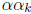. Rather, there is a neater relationship between and .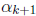

Well, let us go to the induction step. We assume, for some integer k ≥1, that 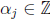  for
1 ≤ j ≤ k. We compute

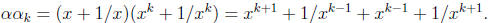
In other words,



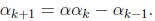
By the (complete) induction step, we know that 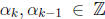, and certainly 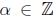so


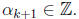
By the principle of complete mathematical induction , we are done.

10. Here is a “proof” by complete induction that all Fibonacci numbers are even! Your
job is to explain the error in the argument.

For n ≥ 0, let P(n) be the statement that 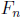is even. We will prove P(n) by complete
induction on n. We check the base case, 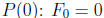  is even. Now we move to the induction
step: We must show that if P(j) holds for 0 ≤ j ≤ n, then P(n) holds. Well, if P(j) holds
for 0 ≤ j ≤ n, then 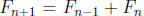is even because 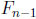and 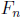are even by P(n − 1)
and P(n), respectively. By Complete Induction, therefore, 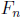is even for all n ≥ 0.

The error is in the step where P(n − 1) and P(n) are both used. For n = 1, this requires
both P(0) and P(1) to be true. So, when one wants to do the base case, one needs to check
both P(0) and P(1). It is not enough to check P(0). Indeed, when one tries to check P(1),
it turns out to be false, for 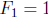is odd.