Straight Lines and Linear Functions
§1.2 Straight Lines
Slope: If L is a line passing through the points
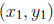 and
and 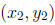 then the slope of L is given by:
then the slope of L is given by:
m = ___.
The slope of a line is a measure of the ___.
Example: Find the slope of the line that passes through the points (−1,
1) and (5, 3).
Example: Sketch the straight line that passes through the point (−2, 5)
and has slope 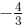 .
.
Example: Find the slope of the line that passes through the points (−2,
5) and (3, 5).
The slope of a horizontal line is ___.
The slope of a vertical line is ___.
Two lines are parallel if their slopes are ___(or
in the case of vertical lines)___.
Example: If the line passing through the points (2,
a) and (4, 9) is parallel to the line passing
through the points (3, 6) and (−1, a + 5), what is the value of a ?
Two nonvertical lines with slopes m1 and m2 are perpendicular if ___.
Point-Slope Form: An equation of the line that has slope m and passes
through the point (x1, y1)
is given by
If you are not given m, but are given 2 points on the line, first find m using
the two points, and then
use Point-Slope Form.
Example: Find an equation of the line that passes through the point (3,
1) and is perpendicular to
the line that passes through the points (−3, 2) and (4,−1).
The x-intercept of a line is the value of x where the line crosses the x-axis.
To find the x-intercept
set ___and solve for x .
The y-intercept of a line is the value of y where the line crosses the y-axis.
To find the y-intercept
set ___and solve for y.
Slope-Intercept Form: The equation of the line that has slope m and
intersects the y-axis at the
point (0, b) is given by
Example: Suppose an art object purchased for
$50,000 is expected to appreciate in value at a
constant rate of $5000 per year for the next 5 years.
(a) Write an equation predicting the value of the art object in the next several
years.
(b) Find the value of the art object 3 years from the purchase date.
Graphing lines on the calculator:
1. Write the equation of the line in slope-intercept form y = mx + b
2. Press Y= and enter in the equation of the line
3. Press WINDOW to adjust the viewing window of the graph
4. Press GRAPH
§1.3 Linear Functions and Mathematical Models
A function f is a ___.
Given a function y = f (x), x is called ___and
y is called ___. The function takes in a value
of x (input) and spits out a value for y (output).
Domain of f is ___.
Range of f is the set of ___.
Example of a function:
Note: Sometimes different letters than x and y are used.
Linear function: The function f defined by ___where m and b are constants is
called
a linear function. The graph of this function is a ___.
Example: A printing machine has an original value of $100,000 and is to
be depreciated linearly
over 5 years with $30,000 scrap value.
(a) Find an expression giving the book value at the end of year t.
(b) What will be the book value of the machine at the end of the second year?
(c) What is the rate of depreciation of the printing machine?
Appreciation: ___slope
Depreciation: ___slope
Linear cost, Revenue, and Profit functions:
If x is the number of units manufactured or sold. Then
Total Cost Function: C (x) = Total cost of manufacturing x units of the
product
Revenue Function: R (x) = Total revenue realized from the sale of x units
of the product
Profit Function: P (x) = Total profit realized from manufacturing and
selling x units of the product
Suppose firm has a fixed cost of F dollars, a production cost of c dollars per
unit, and selling price
of s dollars per unit. Then
C (x) =
R (X) =
P (x) =
Example: A company makes heaters. They find that
the cost to make 10 heaters is $1500 and the
cost to make 20 heaters is $1900. The heaters are sold for $150 each. Find the
cost, revenue, and
profit functions.
What is the production cost per heater? ___What are the fixed costs?___
Linear Demand and Supply curves
A demand equation expresses the relationship between the unit price and
the quantity demand.
In general, the quantity demanded decreases as the unit price increases, and
vice versa. We write
p = f (x) for the demand function, where p measures the unit price and x
is the number of units
demanded. The corresponding graph (only the first quadrant) is called a
demand curve.
A supply equation expresses the relationship between the unit price and
the quantity supplied
from the manufacturer. In general, an increase in the unit price leads to
increase in the supply, and
vice versa. We write p = f (x) for the supply function, where p measures
the unit price and x is
the number of units supplied. The corresponding graph (only the first quadrant)
is called a supply
curve.
Example: (Demand function) The quantity demanded of the Sentinel alarm
clock is 48,000 units
when the unit price is $8. At $12 per unit, the quantity demanded drops to
32,000 units. Find
the demand function, assuming that it is linear. What is the unit price
corresponding to a quantity
demanded of 40,000 units? What is the quantity demanded if the unit price is
$14?
Example: (Supply function) The supply equation for
a commodity is given by 4p−5x = 120, where
p is measured in dollars and x is measured in units of 100.
(a) Sketch the corresponding curve
(b) How many units will be marketed when the unit price is $55?
The slope of a demand curve in general is:___
The slope of a supply curve in general is:___
§1.4 Intersection of Straight Lines
Example: Find the point of intersection of the lines y = x + 1 and y =
−2x + 4 by hand.
Finding the intersection point on your calculator:
1. Press Y = and enter the two equations as Y1 and Y2
2. Press WINDOW and choose appropriate values
3. Press GRAPH
4. Press 2nd and TRACE and choose 5: intersect
5. Select the lines you want to intersect by moving the cursor up or down and
pressing ENTER
5. When it asks you to Guess press ENTER again
Break-Even Analysis
The level of production at which the firm neither makes a profit nor sustains a
loss is called the
break-even level of operation . It is determined by solving the equations p = C (x)
and p = R (x)
simultaneously. The point of intersection 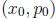 of these two lines is called the break-even point.
of these two lines is called the break-even point.
That is the point when the firm starts to make money. The number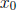 is called the break-even
is called the break-even
quantity and the number 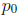 is called the
break-even revenue.
is called the
break-even revenue.
Example: Prescott manufactures its products at a
cost of $4 per unit and sells them for $10 per
unit. If the firm’s fixed cost is $12,000 per month, determine the firm’s
break-even point
What is the loss sustained by the firm if only 1500 units
are produced and sold each month?
How many units should the firm produce to realize a minimum monthly profit of
$9000?
Market Equilibrium
The market is said to be in an equilibrium when ___. The quantity
produced at market equilibrium is called the ___, and the corresponding price is
called the ___. Geometrically, market equilibrium corresponds to the point at
which
the demand curve and the supply curve intersect.
Example: The management of ThermoMaster has determined that the demand
equation for its
products is 5x + 3p − 30 = 0 where p is the price of a thermometer in dollars
and x is the quantity
demanded in units of a thousand. The supply equation for these thermometers is
52x−30p+45 = 0
where x (measured in thousands) is the quantity ThermoMaster will make available
in the market
at p dollars each. Find the equilibrium quantity and price.
§1.5 The Method of Least Squares
The method of least squares is used for determining a straight line that, in
some sense, best fits a
set of data points are scattered about a straight line.
Suppose we are given data points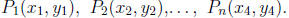 If di is the
vertical distance
If di is the
vertical distance
between the straight line and the given data point Pi, then the principle of
least squares
states that the straight line L that fits the data point best is the one chosen
by requiring that
___.
The line L obtained in this manner is called the least-squares line, or
regression line.
The correlation coefficient r is a measure of how closely the line fits the
data. Its value is always
between ___. The closer r is to 1 or -1, ___. To be able to see r on
your calculator, you must turn Diagnostics on.
How to find the regression line on the calculator:
1. If you need the r value, turn Diagnostics: press 2nd CATALOG , then press D,
scroll down to
Diagnostics On, and press ENTER twice. (You can skip this step if Diagnostics is
on already)
2. Press STAT and choose 1: Edit
3. Enter the first row/column of data under L1 and the second row/column of data
under L2 (You
can clear any lists that are already there by moving the cursor to the L above
that list and pressing
CLEAR, ENTER.)
4. Press STAT the right arrow to the CALC menu. Choose 4: LinReg (ax+b)
You are now on the home screen with LinReg (ax+b) showing
5. Press V ARS then right arrow to Y − V ARS. Choose 1: Function then choose 1:
Y1
You are now on the home screen with LinReg (ax+b) Y1 showing
6. Press ENTER
7. The equation of the line you computed will also be stored under Y1 in the Y =
menu. You can
graph this line now by pressing GRAPH.
8. If you also want to see the scatter plot when you graph, press 2nd Y = or
STATPLOT, select
which plot you want to use, turn this plot ON, and choose the picture that looks
like scatter plot
(the first one). Finally, press GRAPH and adjust the window. (Note: Remember to
go back to
STATPLOT and turn the scatter plot off, or it will be graphed every time and
will cause errors.)
9. If you want to plug in an x value into the regression line, type in Y
1(x−value) and press ENTER.
Alternatively, go to CALC (2nd TRACE) and choose 1: value. Enter the value for
x.
10. To find a x value from your regression line when given a y value, enter the
y value under Y @
and then find the intersection point of Y 1 (the regression line) and Y 2.
Note: If you happen to delete your lists or the calculator is doing something
strange, press STAT,
choose5: SetUpEditor and press ENTER. This will reset your lists.
Example: According to the U. S Department of Energy, the consumption of energy by
countries of
the industrialized world is projected to rise in the future. The consumption (in
trillion cubic feet )
from 2000 through 2025 is summarized in the following table.
| Year | 2000 | 2005 | 2010 | 2015 | 2020 | 2025 |
| Consumption | 214 | 225 | 240 | 255 | 270 | 285 |
Let x be the number of years since 2000.
(a) Find an equation of the regression line for these data. How well does the
line fit the data?
(b) Use the result from (a) to estimate the energy consumption in the
industrialized world in 2012.
Example: According to company reports, Starbucks’ annual sales (in billions of
dollars) for 1998
through 2003 are as follows:
| Year | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 |
| Sales | 1.28 | 1.73 | 2.18 | 2.65 | 3.29 | 4.08 |
(a) Find an equation for the least-squares line for these
data.
(b) Use the result to estimate Sturbucks’ sales for 2008, assuming that the
trend continues.
| Prev | Next |