Textbooks for High School Students Studying the Mathematics
Textbooks for High School Students Studying the Mathematics
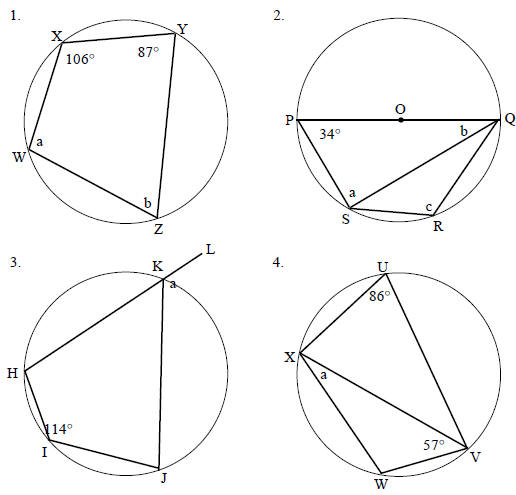
Exercise: Circles IV
1. Find the values of the unknown letters.
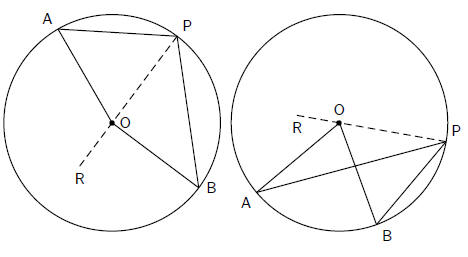
Theorem 14. Two tangents drawn to a circle from the same point outside the
circle are equal
in length.
Proof:
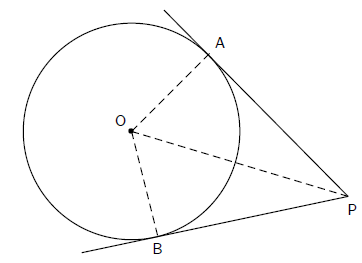
Consider a circle, with centre O. Choose a point P outside the circle. Draw two
tangents to the
circle from point P, that meet the circle at A and B. Draw lines OA , OB and OP.
The aim is to prove that AP = BP.
In △OAP and △OBP,
1. OA = OB (radii)
2.  OAP =
OAP = OPB = 90°(OA ⊥ AP and OB ⊥ BP)
OPB = 90°(OA ⊥ AP and OB ⊥ BP)
3. OP is common to both triangles.
△OAP ≡ △OBP (right angle, hypotenuse, side)
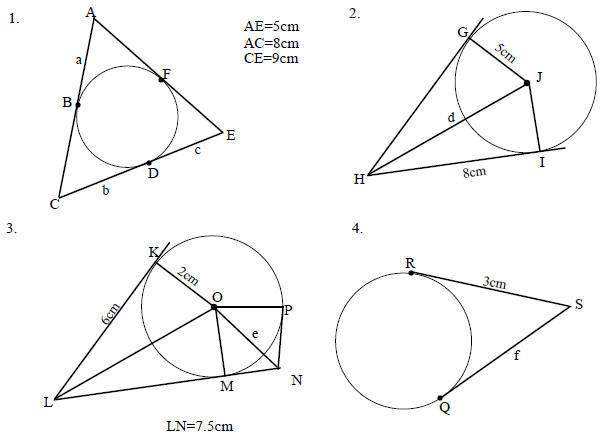
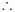 AP = BP
AP = BP
Exercise: Circles V
1. Find the value of the unknown lengths.
Theorem 15. The angle between a tangent and a chord, drawn at the point of
contact of the
chord, is equal to the angle which the chord subtends in the alternate segment.
Proof:
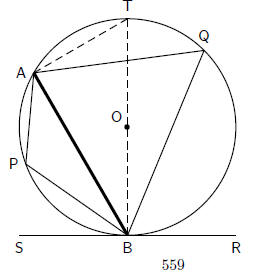
Consider a circle, with centre O. Draw a chord AB and a tangent SR to the circle
at point B.
Chord AB subtends angles at points P and Q on the minor and major arcs,
respectively.
Draw a diameter BT and join A to T .
The aim is to prove that
 and
and 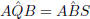 .
.
First prove that 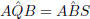 as this result is needed to prove that
as this result is needed to prove that
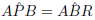

Exercise: Circles VI
1. Find the values of the unknown letters.
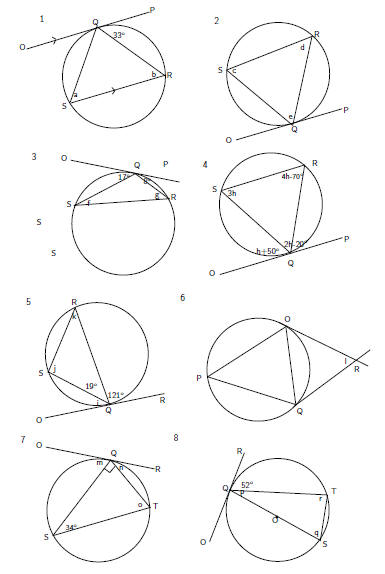
Theorem 16. (Converse of 15) If the angle formed between a line, that is drawn
through the
end point of a chord, and the chord, is equal to the angle subtended by the
chord in the alternate
segment, then the line is a tangent to the circle.
Proof:
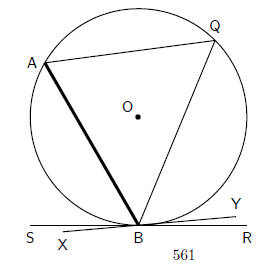
Consider a circle, with centre O and chord AB. Let line SR pass through point B.
Chord AB
subtends an angle at point Q such that 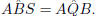
The aim is to prove that SBR is a tangent to the circle.
By contradiction. Assume that SBR is not a tangent to the circle and draw XBY
such that
XBY is a tangent to the circle.
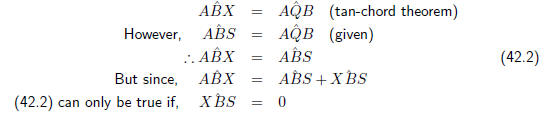
If 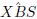 is zero , then both XBY and SBR coincide and SBR is a tangent to the
circle.
is zero , then both XBY and SBR coincide and SBR is a tangent to the
circle.
Exercise: Applying Theorem 9
1. Show that Theorem 9 also applies to the following two cases:
Worked Example 190: Circle Geometry I
Question:
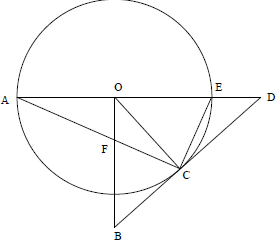
BD is a tangent to the circle
with centre O.
BO ⊥ AD.
Prove that:
1. CFOE is a cyclic quadrilateral
2. FB = BC
3. △COE///△CBF
4. CD2 = ED.AD
Answer
1. Step 1 : To show a quadrilateral is cyclic, we need a pair of opposite
angles to be supplementary, so lets look for that.
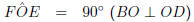
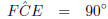 (
(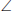 subtended by diameter AE)
subtended by diameter AE)
 CFOE is a cyclic quadrilateral (opposite
CFOE is a cyclic quadrilateral (opposite
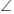 's supplementary)
's supplementary)
2. Step 1 : Since these two sides are part of a triangle, we are proving that
triangle to be isosceles. The easiest way is to show the angles opposite
to those sides to be equal.
Let 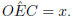
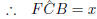 (
(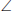 between tangent BD and chord CE)
between tangent BD and chord CE)
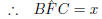 (exterior
(exterior 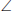 to cyclic quadrilateral CFOE)
to cyclic quadrilateral CFOE)
 BF = BC (sides opposite equal
BF = BC (sides opposite equal
 's in isosceles △BFC)
's in isosceles △BFC)
3. Step 1 : To show these two triangles similar, we will need 3 equal angles.
We already have 3 of the 6 needed angles from the previous question .
We need only find the missing 3 angles.
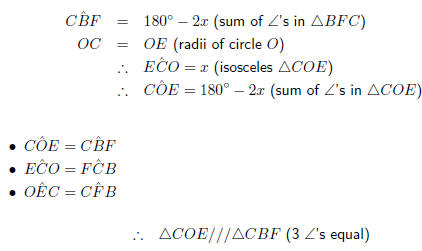
4. Step 1 : This relation reminds us of a proportionality relation between
similar triangles. So investigate which triangles contain these sides and
prove them similar. In this case 3 equal angles works well. Start with
one triangle.
In △EDC
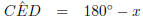 (
(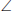 's on a straight line AD)
's on a straight line AD)
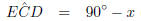 (complementary
(complementary
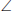 's)
's)
Step 2 : Now look at the angles in the other triangle.
In △ADC
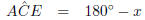 ( sum of
( sum of 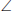 's
's
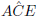 and
and 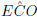 )
)
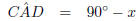 (sum of
(sum of 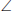 's in △CAE)
's in △CAE)
Step 3 : The third equal angle is an angle both triangles have in common.
Lastly, 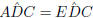 since they are the same
since they are the same
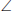
Step 4 : Now we know that the triangles are similar and can use the
proportionality relation accordingly.
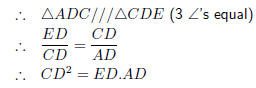
5. Step 1 : This looks like another proportionality
relation with a little
twist, since not all sides are contained in 2 triangles. There is a quick
observation we can make about the odd side out, OE.
OE = CD (△OEC is isosceles)
Step 2 : With this observation we can limit ourselves to proving triangles
BOC and ODC similar. Start in one of the triangles.
In △BCO
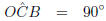 (radius OC on tangent BD)
(radius OC on tangent BD)
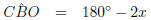 (sum of
(sum of 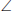 's in △BFC)
's in △BFC)
Step 3 : Then we move on to the other one.
In △OCD
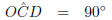 (radius OC on tangent BD)
(radius OC on tangent BD)
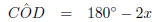 (sum of
(sum of 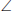 's in △OCE)
's in △OCE)
Step 4 : Again we have a common element .
Lastly, OC is a common side to both △'s.
Step 5 : Then, once we’ve shown similarity, we use the proportionality
relation , as well as our first observation, appropriately.
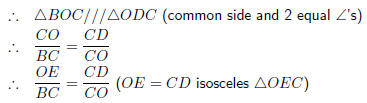
Worked Example 191: Circle Geometry II
Question:
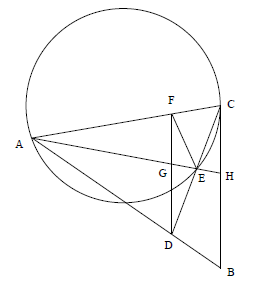
FD is drawn parallel to the
tangent CB
Prove that:
1. FADE is cyclic
2. △AFE///△CBD
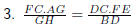
Answer
1. Step 1 : In this case, the best way to show FADE is a cyclic quadrilateral
is to look for equal angles, subtended by the same chord.
Let
 BCD = x
BCD = x
 CAH = x (
CAH = x (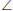 between tangent BC and chord CE)
between tangent BC and chord CE)
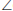 FDC = x (alternate
FDC = x (alternate
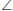 , FD || CB)
, FD || CB)
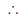 FADE is a cyclic quadrilateral (chord FE subtends equal
FADE is a cyclic quadrilateral (chord FE subtends equal
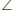 's)
's)
2. Step 1 : To show these 2 triangles similar we will need 3 equal angles.
We can use the result from the previous question.
Let
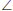 FEA = y
FEA = y
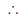
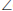 FDA = y (
FDA = y (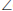 's subtended by same chord AF in cyclic quadrilateral FADE)
's subtended by same chord AF in cyclic quadrilateral FADE)
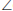 CBD = y (corresponding
CBD = y (corresponding
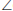 's, FD
|| CB)
's, FD
|| CB)
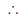
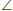 FEA
=
FEA
=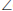 CBD
CBD
Step 2 : We have already proved 1 pair of angles equal in the previous
question.
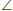 BCD
=
BCD
=
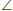 FAE (above)
FAE (above)
Step 3 : Proving the last set of angles equal is simply a matter of adding
up the angles in the triangles. Then we have proved similarity.
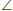 AFE
= 180°-x - y (
AFE
= 180°-x - y (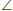 's in △AFE)
's in △AFE)
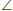 CBD
= 180° x - y (
CBD
= 180° x - y (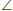 's in △CBD)
's in △CBD)
 △AFE///△CBD (3
△AFE///△CBD (3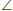 's equal)
's equal)
3. Step 1 : This equation looks like it has to do with proportionality relation
of similar triangles. We already showed triangles AFE and CBD similar
in the previous question. So lets start there.
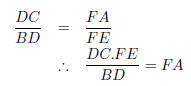
Step 2 : Now we need to look for a hint about side FA. Looking at
triangle CAH we see that there is a line FG intersecting it parallel to
base CH. This gives us another proportionality relation .
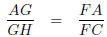 (FG
|| CH splits up lines AH and AC proportionally)
(FG
|| CH splits up lines AH and AC proportionally)
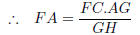
Step 3 : We have 2 expressions for the side FA.
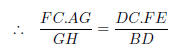
| Prev | Next |