Standard Form of a Circle
12.3 The Circle
The next conic that we would like to examine is the circle
Standard form of a Circle
Let r be the radius of a circle and let (h, k) be the
center of the circle. Then the equation of the
circle is (x - h)2 + (y-k)2 =r2
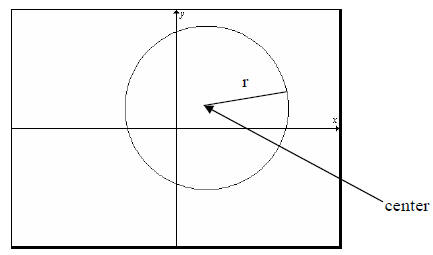
Graphing a circle is fairly easy. All we need to do is get
the equation into standard form and then
plot the center and use the radius to determine the rest. We will also want to
find the x-and y-
intercepts.
Example 1:
Graph the following. Find all x and y-intercepts.

Solution :
a. Since the equation is already in standard form, we can simply read off the
center of the circle.
Notice that the equation is (x - h)2 + (y-k)2 =r2
and the center is (h, k),. That means
the center is (1, -2) in our case. We can also read off the radius. Since we see
that
r2 = 25 we clearly have r=5 . Now to graph, we simply plot the
center and go out from it 5
units in each direction. We get the following graph
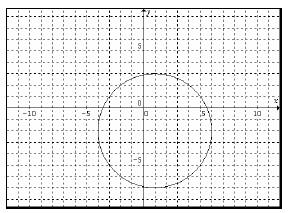
Now we still need to find the x- and y-intercepts. We do
this the same way we always have.
For x-intercepts, set y = 0 and for y-intercepts, set x = 0.
x-intercepts
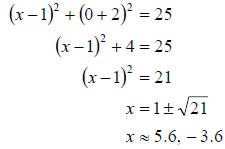
y-intercepts:
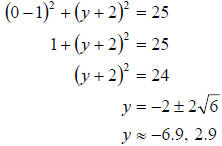
Looking at the graph again we can see clearly these are
the correct values.
b. This time we are not given the equation in such a nice form. We will need to
put the equation
into standard form in order to get the important information. To do that, we
will complete the
square just like in the previous section . However, this time, since we want to
have the radius
on the right hand side, we will add our completed square portion to both sides
instead of
adding it in and then subtracting it off of the same side as we did with the
parabola. We
proceed as follows
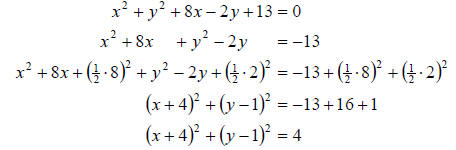
Now we can clearly see that the center is (-4,1)− and the
radius is r=2.
So we graph the circle by plotting the center and going out 2 units in each
direction. We
get
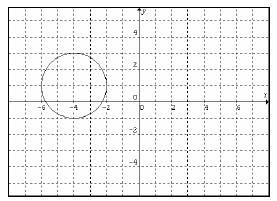
Lastly we need to find the x- and y-intercepts.
We can see from the graph that we should have two x -intercepts and no
y-intercepts
since it hits the x-axis twice and does not hit the y-axis at all. Lets verify
this with usual
steps .
x-intercepts:
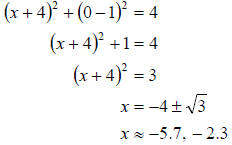
y-intercepts:
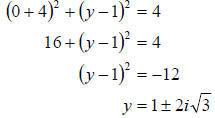
So we can see that since we get imaginary values for our
y -intercepts, we have no y-
intercepts, just as our graph had indicated.
One of the main things that we want to do in this chapter is to be able to
distinguish between the
various conics from the very beginning of the problem. So far the only conics
that we have are
the parabola and circle . It is very easy to tell a parabola from all the other
conics, since the
parabola will be the only one that only has one variable that is squared .
So, at the moment we have the following
Only one of the two variables is squared- the conic is a parabola
Both variables are squared- the conic is a circle
12.3 Exercises
Graph the following. Identify the center, radius and all x and y-intercepts.

Identify if the following is a parabola or a circle. Then
graph accordingly.
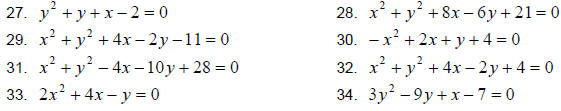
Find the equation of the circle that satisfies the given
conditions.
35. center (-1, 3), r =3
36. center (2,-5), r=4
37. center (−1, 1)and point(3,4) is on the circle
38. center(−2,-3) and point (1,1) is on the circle
39. (-1,1)and (3,4)are endpoints of the diameter
40. (-2.-3)and (1,1)are endpoints of the diameter
41. center ( -2,1)and one y- intercept is at -3
42. center (4,-5) and one x-intercept is at 3
Find the area of the following circles.
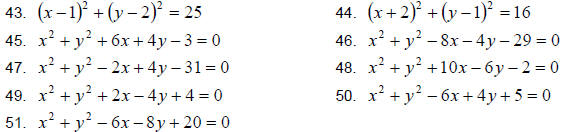
| Prev | Next |