Elimination and Matrix Operations
Essay Questions
Read Carefully! You have the weekend to complete the exam. The exam is
due, on my desk, at the
beginning of class on Monday.
This exam is open notes, open book. All work must be done by hand, but you
may certainly use a
calculator or computer to check your work where appropriate. You must answer all
of the exercises on your
own. You are not allowed to work in groups on the exam . You are not allowed to
enlist the aid of a tutor
or friend to help with the exam. You are not allowed to read the exercises in
the exam, then seek help on
similar questions. Once you open the exam and read the questions, you may not
seek any outside help of
any kind. From the moment you open the exam, you must do everything by yourself.
Place the solution to each exercise on a separate sheet of paper. On a good
sheet of paper, write out
(longhand) and sign the following honor pledge.
I promise that all work found herein is my own. I have received no help from
tutors, colleagues,
or other teachers. I have honored all of the examination constraints listed in
the directions.
Arrange the problems in order, place these examination pages on top of your
solutions, then place the honor
pledge on top of the examination as a cover sheet. Staple. Good luck!
Exercise 1. Use elimination and back substitution to solve the
following system of equations. All computations
are to be performed by hand. Show your work.
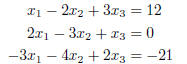
Exercise 2. The following matrix represents the reduced row echelon
form of an augmented matrix for a
system of three equations in unknowns x1, x2 and x3.

What is the solution of the system?
Exercise 3. Let A be a matrix with three rows.
(a) What 3×3 matrix E adds 5 times row 2 to row 3 and then adds 2 times row 1
to row 2, when it multiplies
matrix A?
(b) What 3 × 3 matrix F subtracts 2 times row 1 from row 2 and then subtracts
5 times row 2 from row 3,
when it multiplies matrix A? How is F related to matrix E in the previous
question?
Exercise 4. Consider the coefficient matrix
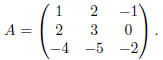
For what triples
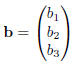
does the system Ax = b have a solution?
Exercise 5. Suppose that A is a 4×4 matrix such that the sum of the
first two columns of matrix A equals
the sum of columns 3 and 4.
(a) Find a nonzero solution of Ax = 0, where x is a column vector.
(b) Explain why matrix A is noninvertible (singular).
Exercise 6. Suppose that B is a 5×5 matrix so that the sum of the first two
rows of B is 3 times the sum
of rows 3, 4, and 5. Find a nonzero solution of yB = 0, where y is a row vector.
Exercise 7. Show how you can express matrix

as the product of two vectors .
Exercise 8. Let
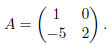
(a) Find elementary matrices E and F so that EFA = I.
(b) Write A-1 as a product of elementary matrices.
Exercise 9. You learned in class that you can find the inverse of a 2 × 2 matrix with the formula
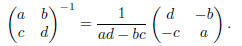
Use this formula to find the inverse of the matrix
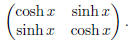
Hint: The hyperbolic cosine and sine are defined as follows:
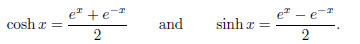
Exercise 10. Given that
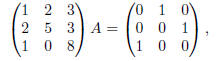
find A-1. Note: This problem is trivial if approached in the correct manner.
Look for an elegant solution.
Little credit will be given for crunch and grind solutions.
Exercise 11. For what value(s) of c is matrix A singular (not invertible)?
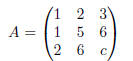
Exercise 12. Four by four matrix A consists of four 2 × 2 blocks.
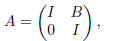
where I is the 2 × 2 identity matrix, 0 is a 2 × 2 zero matrix (all entries
are zeros), and B is any 2 × 2
invertible matrix.
(a) In block notation, what is the inverse of matrix A?
(b) Craft a 4 × 4 matrix A that adheres to the pattern described above. Use the
technique developed in
part (a) to find the inverse of your example.
(c) Use your matrix A from part (b), set up the augmented matrix [A I] and use
row reduction to place your
augmented matrix in the form [I A-1]. This result should agree with the solution
found in part (b)?
Solutions to Exercises
Exercise 1. Take the system
x1 − 2x2 + 3x3 = 12
2x1 − 3x2 + x3 = 0
−3x1 − 4x2 + 2x3 = −21
and set up the augmented matrix
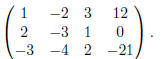
Subtract 2 times row 1 from row 2. Subtract −3 times row 1 from row 3.
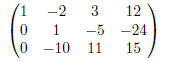
Subtract −10 times row 2 from row 3.
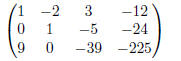
This matrix represents the equivalent system

We use back substitution to find the solution . Solve (3) for x3.
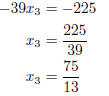
Substiute x3 = 75/13 in (2) and solve for x2.
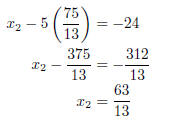
Substitute x 3 = 75/13 and x2 = 63/13 in (1) and solve for x1.
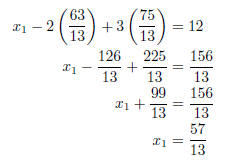
Thus, the solution is
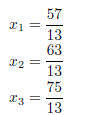
Exercise 2. The augmented matrix

represents the system
x1 + 2x2 = 3 (4)
x2 + 3x3 = 4, (5)
where x1 and x2 are pivot variables and x3 is a free variable. Solve (4) and
(5) for the pivot variables. This
gives solution
x1 = 3 − 2x3
x2 = 4 − 3x3
x3 = free.
Exercise 3(a) The elementary matrix
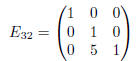
adds 5 times row 2 to row 3 of matrix A when applied in the order E 32A. The elementary matrix
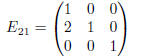
adds 2 times row 1 to row 2 of E32A when applied in the order E21E32A. Hence, the matrix we seek is
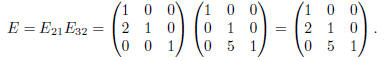
Exercise 3(b) The elementary matrix
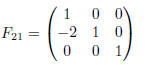
subtracts 2 times row 1 from row 2 of matrix A when applied in the order F21A. The elementary matrix
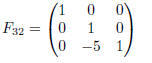
subtracts 5 times row 2 of F21A when applied in the order F32F21A. Hence, the matrix we seek is
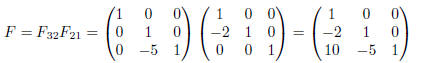
Because the marix F reverses the steps of matrix E in inverse order, it must
be the case that F is the inverse
of matrix E. This is easily checked. Note that
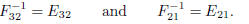
Hence, these relations provide
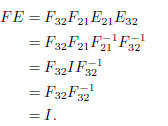
Similarly, it can be shown the EF = I. Hence, F and E are inverses of one another
Exercise 4. Set up the augmented matrix
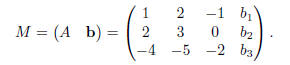
Subtract 2 times row 1 from row 2. Subtract −4 times row 1 from row 3.
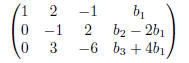
Subtract −3 times row 2 from row 3.
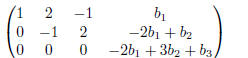
Because the last equation of the system represented by this matrix is
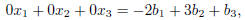
the system will have solutions if and only if
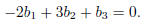
Exercise 5(a) Matrix A has the form
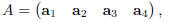
where we’re given that
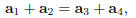
or, equivalently,
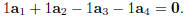
Clearly, x = (1, 1,−1,−1)T is a solution, as
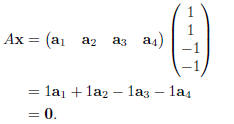
Exercise 5(b) Suppose, for purposes of contradiction, that A is invertible. Then A-1 exists and
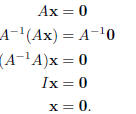
This says that the only solution of Ax = 0 is x = 0, which
contradicts the finding in part (a). Thus, A is
not invertible.
Matrix B has the form
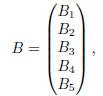
where
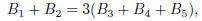
or, equivalently,
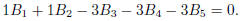
Clearly, y = (1, 1,−3,−3,−3) is a solution as
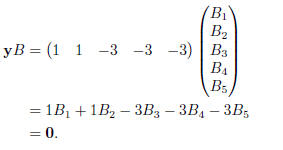
Exercise 7. Using block multiplication,
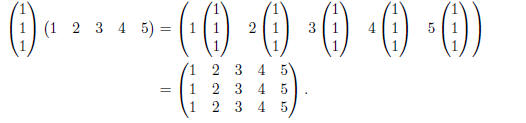
Exercise 8(a) Let
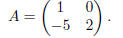
Subtract −5 times row 1 from row 2.

Now, multiply the second row of FA by 1/2.
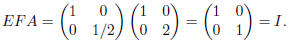
Exercise 8(b) Hence,
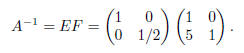
Exercise 9. We will use the formula
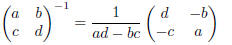
to invert
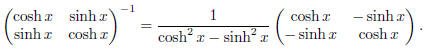
However,
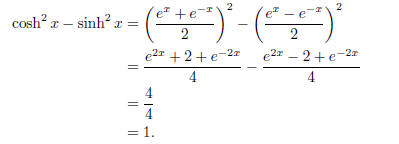
Hence,
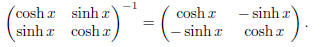
Exercise 10. We’re given that
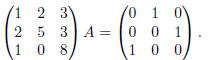
To find an inverse, we need the right-hand side of
equation (6) to equal the identity matrix I. First, swap
rows 1 and 3.
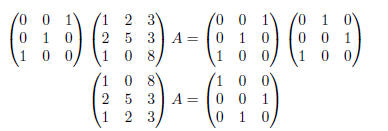
Next, sqap rows 2 and 3.
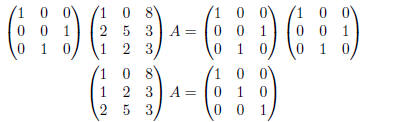
Equivalently,
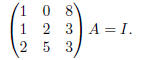
Thus,
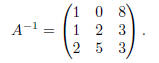
Exercise 11. We attempt to tow reduce matrix
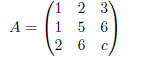
to the identity. Subtract 1 times row 1 from row 2. Subtract 2 times row 1 from row 3.
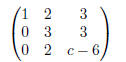
Subtract 2/3 times row 2 from row 3.
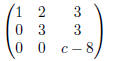
If c = 8, then the entry in row 3, column 3 will be zero
and there is no hope of continuing the reduction to
the identity matrix. Hence, if c = 8, matrix A is not invertible.
Exercise 12(a) To find the inverse of matrix
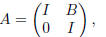
we first craft the augmented matrix
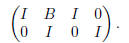
We must reduce A to the identity matrix. Subtract B times row 2 from row 1.
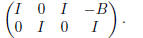
Hence,
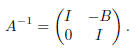
Exercise 12(b) Consider
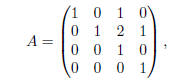
which in block form, has the form
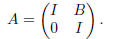
By part (a),
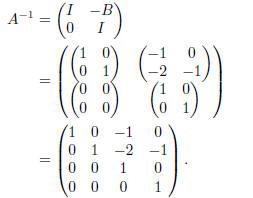
Exercise 12(c) Set up

Subtract 1 times row 4 from row 2.

Subtract 2 times row 3 from row 2. Subtract 1 times row 3 from row 1.

Hence,
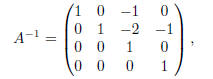
which agrees with the result found in part (b).
| Prev | Next |