The Cubic Equation

[Pinter, Charles C. A Book of Abstract Algebra , McGraw-Hill, Inc. New
York, 1990.]

Recall the quadratic formula solved for the roots of a quadratic polynomials;
that is polynomials of the form

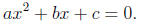
All the roots are given by the formula:

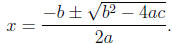
There is a general formula for cubic polynomials , those of the form

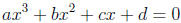
and the quartic

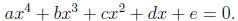
However there can be no other formulas – in part because any number
greater than 4 determines certain things called groups with properties related
to polynomials that can never be fixed.  Here we will explore the
cubic equation.

To begin with, any cubic polynomial can be written as

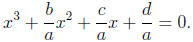
For convenience we will relabel our letters as

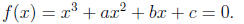
1. Begin by substituting 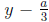in for x. You may want to try this with
some actual numbers first . Once you have checked you will realize
that

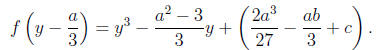
Notice the x² term is gone ! This trick is incredibly useful because
now instead of finding roots of f(x) we will only care about roots of

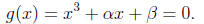
Keep in mind the roots of g will be different form those of f, but we
know that 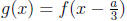so we can go back at the end.

2. Finally g(x) is a nicer polynomial, nice enough to have a cubic formula.
One of the roots will be given as

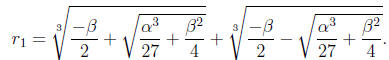
It is particularly more difficult to derive this formula but you may check
with some polynomials to see that you agree.

3. You have one root 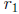so you can divide you polynomial g(x) by
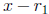
to get a quadratic polynomial . Here you simply use the quadratic
equation to solve for the remaining roots.

4. Now you have to translate all the roots into roots for f(x) by subtracting
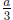from each.