The Euclidean Algorithm
The Euclidean Algorithm and prime field arithmetic |
||
The GCD • gcd(n, m), is the greatest common divisors of n , m: –gcd(n, m) = MAX { d; d divides n & m} • Fact: – If c = gcd(n, m), – and b divides both n and m, – then b also divides the g.c.d. c. |
||
Computing the g.c.d. • The g.c.d. of two numbers can be computed using the Euclidean algorithm • Based on the fact that, given a linear combination: –a = mb + c • then gcd(a, b) = gcd(b, c) |
||
Integer long division • Given a and b, there are values q and r, called the quotient and remainder of the division of a by b such that: – r ≥ 0; – r < |b|; – a = b q + r |
||
Euclides’ Algorithm for g.c.d. • Given n and m, find g.c.d. of n, m. GCD(n, m) IF m = 0 RETURN n r ← REMAINDER(n, m); RETURN GCD(m, r); |
||
Examples
|
||
The GCD as a linear function • The Euclides algorithm has the following property: – Each new recursive invocation has parameters n’, m’ which are a linear transformation of the parameters n, m of the current function call. • n’ = m • m’ = REMAINDER(n,m) = 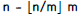 |
||
Backtracking • Since in each step the next set of parameters are a linear combination of the previous set , each set of parameters is a linear combination of the initial parameters (by induction). – Initial set of parameters: n, m – Final set of parameters: c, 0, where c = GCD(n, m) • So c = a n + b m, and a and b can be computed by recording the intermediate transformation taken by the algorithm. |
||
Extended g.c.d. algorithm • Define values a, b, c, d such that, in the i-th step of the GCD computation: 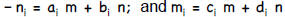 • EXT-GCD(n, m, a, b, c, d) IF m = 0 RETURN n, a, b r ← REMAINDER(n, m) = n - q m RETURN EXT-GCD(m, n-qm, c, d, a-qc, b-qd) |
||
Example • GCD(12, 9,1,0,0,1) FALSE ← IF(9 = 0) r ← 3 = REMAINDER(12,9) = 12 - 1 * 9 (q = 1) RETURN GCD(9, 3, 0, 1, 1, -1) • GCD(9, 3, 0, 1, 1, -1) FALSE ← IF(3 = 0) r ← 0 = REMAINDER(9, 3) = 9 - 3 * 3 (q = 3) RETURN GCD(3, 0, 1, -1, -3, 4) • GCD(3,0) TRUE ← IF(0 = 0) RETURN 3, 1, -1
|
||
Modular arithmetic Finite number sets |
||
Rings • A commutative ring is a set S with two arithmetic operations : – Addition: + – Multiplication: · • and two special elements: – Additive identity: 0 – Multiplicative identity : 1, Id, e |
||
Ring properties • Associativity of addition and multiplication: – a + (b+c) = (a+b) + c; a · (b · c) = (a · b) · c • Commutativity of addition and multiplication: – a + b = b + a; a · b = b · a; • Identity elements: – a + 0 = a = 0 + a; a · Id = a = Id · a; • Additive inverse: – For each a, there is a’ such that a + a’ = 0 • Distributivity: – a · (b + c) = a · b + a · c |
||
Examples of rings • The set of integer Z, rational Q , real R, and complex C numbers. • Non-commutative rings are rings where only addition is commutative. – Example: The set of n×n matrices is a non-commutative ring. • If multiplication is both commutative and has an inverse, i.e: – For each a ≠ 0, there is a* such that a · a* = 1 then we say that the ring is a field. • The rings of rational Q, real R, and complex C numbers are fields, but not the ring of integers Z. |
||
Finite rings • If m is an integer, then for all other integers n, the function – REMAINDER(n, m) has values in the set {0, 1, ..., m-1} • We wish to define a ring structure in the above set, which we will call Zm. • We need to define addition and multiplication operations within Zm. |
||
Remainder addition • if r = REMAINDER(a, m), and s = REMAINDER(b, m) then: – r = a - pm, and s = b - qm for some p, q. – Consider t = REMAINDER(r ± s, m) • t = REMAINDER(a - pm ± (b - qm), m) • t = REMAINDER(a ± b - pm ± (-qm), m) • t = REMAINDER(a ± b, m) • Define r ± s in Zm as – REMAINDER(r ± s, m). |
||
Remainder addition properties • The addition/ subtraction of remainders value (previous slide) must have the same properties of addition /subtraction of integers, because to add/subtract two remainders we can first substitute the remainders by integers, add/subtract them and then take the remainder. • Multiplication of REMAINDERS is defined analogously. |
||
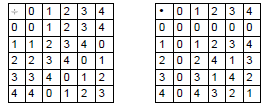
Example: Z5
|
||
Non- zero elements and multiplication • The multiplicative table of Z5 shows that it is a field, because every nonzero element has an inverse: – 2 * 3 = 4 * 4 = 1 * 1 mod 5 • This is not true of all remainder rings:
|
||
Remainder fields • When is the set Zm a field? • For an element n to be inversible mod m, there must exist p such that: – n · p = 1 mod m; this is equivalent to – n p - km = 1, for some k, which is the same as: – gcd(n, m) = 1 |
||
The fields Zm • If Zm is to be a field, then every nonzero remainder r must have – gcd(r, m) = 1 • In particular, gcd(r, m) = 1 for – r = 2, 3, ..., m - 1. • This means that m must be a prime number. |
||
Dividing in Zm • Whether or not m is a prime and Zm a field, in order to compute division a/b in Zm. – a/b := a · (inverse of b) = a · b-1 – b-1 = c such that b * c + k m = 1 – c is the coefficient that is computed using extended g.c.d algorithm: – ext-gcd(b, m) = 1, c, k |
||
Cryptography and modular arithmetic • In cryptography, two types of remainder rings are very important – The field Zp , when p is a prime. – The ring Zn , when n = p q is a product of two primes • We will see these examples when discussing the RSA algorithm. |
| Prev | Next |