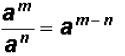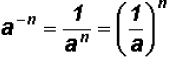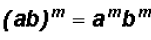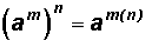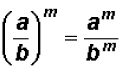The Laws of Exponents
PLEASE NOTE THAT YOU CANNOT USE A CALCULATOR ON THE
ACCUPLACER -
ELEMENTARY ALGEBRA TEST ! YOU MUST BE ABLE TO DO THE FOLLOWING PROBLEMS
WITHOUT A CALCULATOR!
Please be aware that the letters a, b, m , and n are
replacements for any real number .
However, when the letters are identical, we must use the SAME number
replacement!
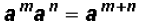
When an exponential expression is
When an exponential expression is divided
When a number is raised to a negative |
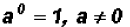
Any number, except for 0, raised to the zero
When a product is raised to a power, each
When an exponential expression is raised
When a fraction is raised to a power, this |
Problem 1:
Multiply
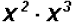
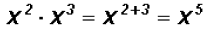
Problem 2:
Multiply
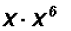
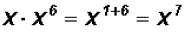
Problem 3:
Multiply
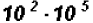
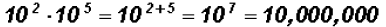
NOTE: 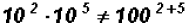
Problem 4:
Multiply
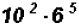
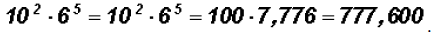
NOTE:
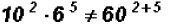
Please note that the law tells us that we have to have
identical numbers
in the base before we can add the exponents.
Problem 5:
Multiply
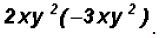
When you are multiplying two or more terms containing
variables , the
operation becomes easier if you group together the numbers and the
exponential expressions with like base and like powers as follows:
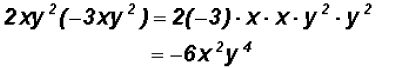
NOTE: You do not have to write down the "grouping"
step . Instead you
can write the answer right away.
Problem 6:
Multiply
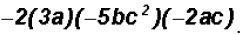
This multiplication becomes easier to group as follows:
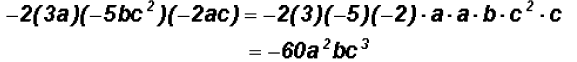
Problem 7:
Multiply
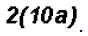
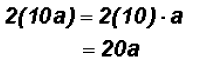
Problem 8:
Divide
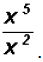
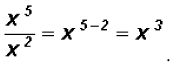
Problem 9:
Divide
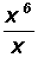
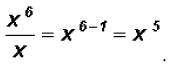
Problem 10:
Divide
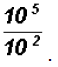
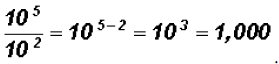
NOTE:
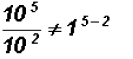
Problem 11:
Divide
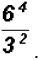
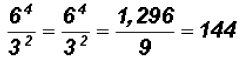
NOTE:
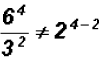
Problem 12:
Divide
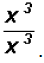
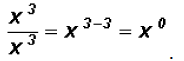
This immediately allows us to illustrate the law
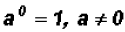 , which states
, which states
that any number raised to the zero power results in a value of 1.
Therefore, 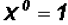 . Please
note that
. Please
note that 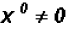 .
.
Problem 13:
Find the value of 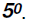
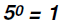
Problem 14:
Find the value of 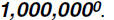
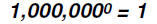
Problem 15:
Find the values of 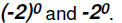
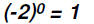
Please note that 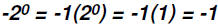
By the Order of Operation , exponential expressions are
simplified BEFORE we multiply
(in this case by -1)!
Problem 16:
Divide
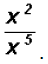
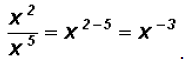
This immediately allows us to illustrate the law
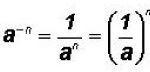 , where the
, where the
negative exponent indicates that the exponential expression is actually in the
denominator of a fraction with numerator 1. Then, when written as a fraction,
the negative sign in the exponent changes to a positive sign.
Therefore, 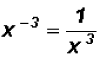 . Please
note that
. Please
note that  .
.
Problem 17:
Rewrite in terms of positive exponents:
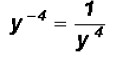
Problem 18:
Rewrite in terms of positive exponents: 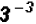
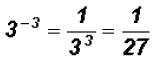
Problem 19:
Rewrite in terms of positive exponents: 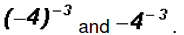
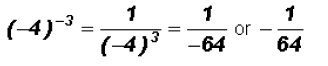
Now observe, 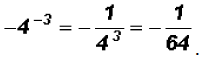
Here we actually have 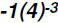 and we have to go by the Order of Operation.
and we have to go by the Order of Operation.
Problem 20:
Rewrite in terms of positive exponents: 
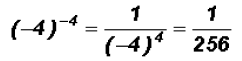
Now observe, 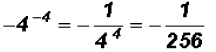
Here we actually have 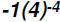 and we have to go by the Order of Operation.
and we have to go by the Order of Operation.
Problem 21:
Divide
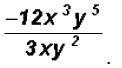
Here we must group together the numbers and the
exponential expressions
with like base as follows:
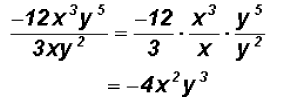
NOTE: You do not have to write down the "grouping"
step. Instead you
can write the answer right away.
Problem 22:
Divide
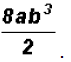
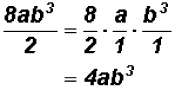
Problem 23:
Divide 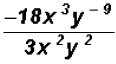 . Write your
answer with positive exponents only!
. Write your
answer with positive exponents only!
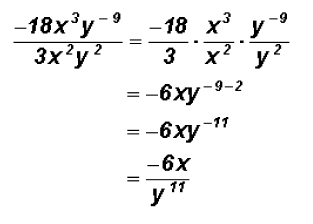
Problem 24:
Divide
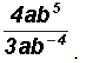
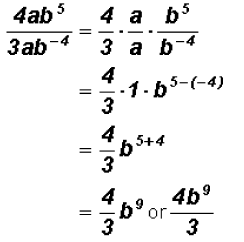
Problem 25:
Simplify 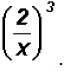
The word "simplify" takes on many meanings in
mathematics. Often you must
figure out its meaning from the mathematical expression you are asked to
"simplify." Here we will be asked to "simplify" instead of finding the value of
the
number raised to the third power.
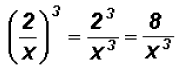
Problem 26:
Simplify 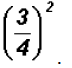
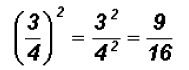
Problem 27:
Simplify 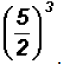
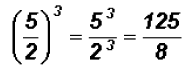
Problem 28:
Simplify 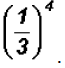
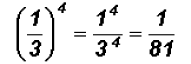
Note that the number 1 raised to any power will always have a value of 1.
Problem 29:
Simplify
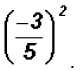
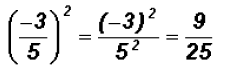
Problem 30:
Simplify
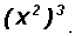
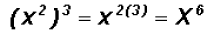
Note that 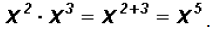
Problem 31:
Simplify
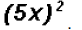
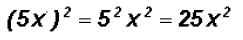
Please note that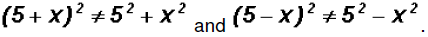 Later
on
Later
on
we will learn how to deal with sums and differences raised to a power!
Problem 32:
Simplify
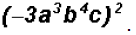
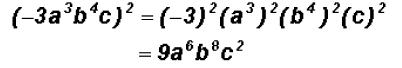
Please note that this law extends to any product
containing infinitely many
factors.
Problem 33:
Simplify
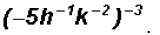
then 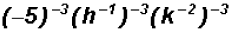
and 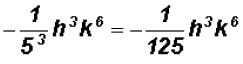
| Prev | Next |