A Math Primer

Systems of Linear Equations

A. The Solutions of a System of Equations
A system of equations refers to a number of
equations with an equal number of variables . We will
only look at the case of two linear equations in two
unknowns. The situation gets much more complex as
the number of unknowns increases , and larger
systems are commonly attacked with the aid of a
computer.

A system of two linear equations in two unknowns
might look like

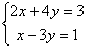
This is the standard form for writing equations when
they are part of a system of equations: the variables
go in order on the left side and the constant term is
on the right. The bracket on the left indicates that the
two equations are intended to be solved
simultaneously, but it is not always used.

When we talk about the solution of this system of
equations, we mean the values of the variables that
make both equations true at the same time. There
may be many pairs of x and y that make the first
equation true, and many pairs of x and y that make
the second equation true, but we are looking for an x
and y that would work in both equations. In the
following pages we will look at algebraic methods
for finding this solution, if it exists.

Because these are linear equations, their graphs will
be straight lines. This can help us visualize the
situation graphically. There are three possibilities:

1. Independent Equations
Lines intersect
One solution

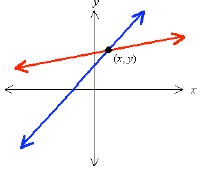
In this case the two equations describe lines that
intersect at one particular point. Clearly this point is
on both lines, and therefore its coordinates (x, y) will
satisfy the equation of either line. Thus the pair (x, y)
is the one and only solution to the system of
equations.

2. Dependent Equations
Equations describe the same line
Infinite number of solutions

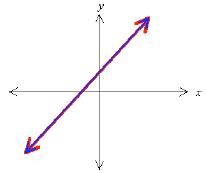
Sometimes two equations might look different but
actually describe the same line. For example, in

The second equation is just two times the first
equation, so they are actually equivalent and would
both be equations of the same line. Because the two
equations describe the same line, they have all their
points in common; hence there are an infinite number
of solutions to the system.

Attempting to solve gives an identity
If you try to solve a dependent system by algebraic
methods, you will eventually run into an equation
that is an identity. An identity is an equation that is
always true, independent of the value(s) of any
variable(s). For example, you might get an equation
that looks like x = x, or 3 = 3. This would tell you
that the system is a dependent system, and you could
stop right there because you will never find a unique
solution.

3. Inconsistent Equations
Lines do not intersect (Parallel Lines; have the
same slope)
No solutions

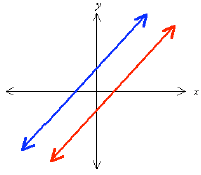
If two lines happen to have the same slope, but are
not identically the same line, then they will never
intersect. There is no pair (x, y) that could satisfy
both equations, because there is no point (x, y) that is
simultaneously on both lines. Thus these equations
are said to be inconsistent, and there is no solution.
The fact that they both have the same slope may not
be obvious from the equations, because they are not
written in one of the standard forms for straight lines.
The slope is not readily evident in the form we use
for writing systems of equations. (If you think about
it you will see that the slope is the negative of the
coefficient of x divided by the coefficient of y).

∞ Attempting to solve gives a false statement
By attempting to solve such a system of equations
algebraically, you are operating on a false
assumption—namely that a solution exists. This will
eventually lead you to a contradiction: a statement
that is obviously false, regardless of the value(s) of
the variable(s). At some point in your work you
would get an obviously false equation like 3!=!4.
This would tell you that the system of equations is
inconsistent, and there is no solution.

Solution by Graphing
For more complex systems, and especially those that
contain non-linear equations, finding a solution by
algebraic methods can be very difficult or even
impossible. Using a graphing calculator (or a
computer), you can graph the equations and actually
see where they intersect. The calculator can then give
you the coordinates of the intersection point. The
only drawback to this method is that the solution is
only an approximation, whereas the algebraic method
gives the exact solution. In most practical situations,
though, the precision of the calculator is sufficient.
For more demanding scientific and engineering
applications there are computer methods that can find
approximate solutions to very high precision.