Algebra Homework #4 Solutions

3.11 Claim: Let G be a group. Then the set Aut(G) of group automorphisms of G forms a group
under composition.

Proof. We need to verify the group axioms for the set Aut(G) under the operation of composition .
First, we show that Aut(G) is closed under composition. We’ll need the following:

Lemma: Let 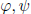: G → G be maps. Then
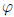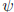i) if and are injective then so is ,
ii) if 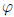and 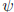are surjective then so is ,
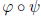iii) if 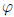and 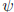are bijective then so is ,
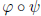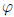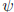iv) if and are group homomorphisms then so is ,
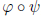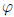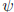v) if and are group isomorphisms then so is .

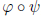Proof. To i), let x, y ∈ G, then

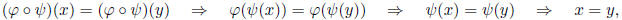
where the second and third implications follow if 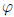and 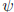are injective, respectively. Thu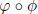s is
injective.

To ii), let x ∈ G, then since is surjective, there exists x' ∈ G such that 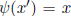. Since 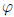is
surjective, there exists x'' ∈ G such that 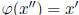. But then

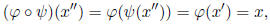
so we see that 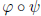is surjective.
To iii), combine i ) and ii).
To iv), let x, y ∈ G, then

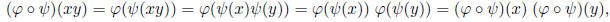
if both 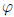and 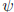are homomorphisms. So we indeed see that 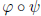is a homomorphism.
To v), combine iii ) and iv).

Thus we see that for automorphisms 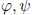, ∈ Aut(G) the composition 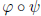∈ Aut(G) is again an
automorphism, so Aut(G) is closed under composition.

Next we quickly verify that composition is associative. For 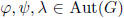and for x ∈ G we
have

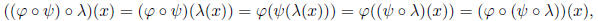
so that indeed 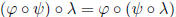, so composition is associative.

Next, we find an identity. Let id : G → G be the identity function, which is clearly an automorphism.
For 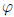∈ Aut(G) and for x ∈ G note that

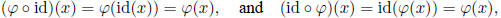
so that indee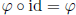d   and 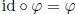. Thus id ∈ Aut(G) is indeed an identity.

Finally, we check that inverses exist, but we already did this in exercise 3.5. For an isomorphism
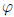: G → G, we previously showed that the inverse function 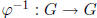is again an isomorphism,
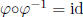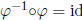and by definition satisfies and , so 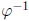is an inverse of 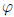for composition. So
indeed, Aut(G) has inverses. We’ve finished showing that Aut(G) is a group under composition.

3.14 Determining some automorphism groups.

a) We’re already show that Aut(Z) = {±id} in exercise 4.4.
b) Since Z/10Z is a cyclic group generated by 1, any homomorphism 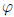: Z/10Z → Z/10Z
is completely defined by the image of 1. Now we also know by exercise 3.6a that if 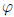is an
isomorphism, then it preserves orders of elements , i.e. 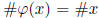for all x ∈ Z/10Z. In
particular, a generator must be sent to a generator. Now in exercise ∈.16b, we already know
that the only elements in Z/10Z that generate are 1, 3, 7, 9. It’s also easy to see that each of
the four choices of where to send 1 gives an automorphism of Z/10Z, so we’ll label them
accordingly:

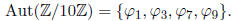
Note that 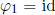. Now we compute the group structure on Aut(Z/10Z). For example, for
x ∈ Z/10Z, we have

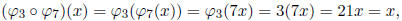
so we find that 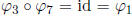. Continuing like this we can calculate the multiplication
table for Aut(Z/10Z):

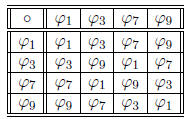
Notice that we have a nice group isomorphism

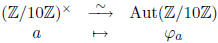
We also see that both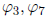 ∈ Aut(Z/10Z) have order 4, i.e. they each generate. This shows
that Aut(Z/10Z) is cyclic, and we can construct two different isomorphisms

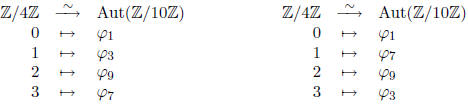
neither of which seems particularly appealing, but just illustrates the two ways we can force
ourselves to think of Aut(Z/10Z) as a cyclic group of order 4.

c) Writing  , we see that the symmetric group
is generated by elements s, t or orders 2, 3, respectively, subject to a further relation. Any
automorphism 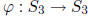is determined by the images of s, t, and as before, must preserve
the orders of elements . Now 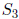has three elements s, st, st² of order 2, and two elements t, t²
of order 3. So any automorphism must take s to one of s, st, s² and t to one of t, t². There
are only six conceivable ways of doing this:

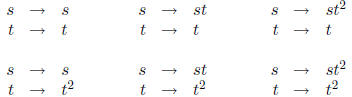
One now checks that each of these in fact does give an automorphism of 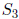. Thus Aut()
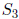just consists of these six elements. We would further like to know the structure of Aut().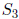
One way to do this is to know that there are only two isomorphism classes of groups of
order six , namely cyclic of order six and 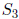. We then just need to check if two of these
automorphisms don’t commute. In fact 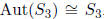Another way to see this is to note
that the center Z(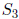) is trivial, so that conjugation by each element of 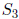gives a different
automorphism, since there are already six of these, these fill up all of Aut(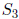). Thus we have
the nice isomorphism

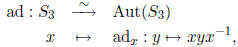
in the notation from lab.

d) The analysis of Aut(Z/8Z) follows exactly the same way as for Aut(Z/10Z) in part b). In
the end, we find that Aut(Z/8Z) = 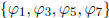and we have the nice isomorphism

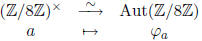
Incidentally, we check that each element of Aut(Z/8Z) has order two, so that Aut(Z/8Z)
Z/∈Z × Z/∈Z.

e) Is the automorphism group of a cyclic group necessarily cyclic? Well, no, see part d).
f) Is the automorphism group of an abelian group necessarily abelian? Well, no either. Take for
example the abelian group 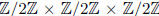Each permutation of the entries gives a
group automorphism, and as we know, permutations of three objects don’t usually commute.
In particular, we see that Aut(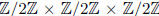) has a subgroup isomorphic to the
permutation group 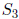. Do you think that is the whole automorphism group?

4.8 Subgroups of groups.
a) The subgroups of 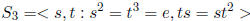 are:

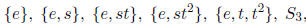
and {e}, {e, t, t²}, 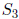are normal subgroups.
b) The subgroups of the quaternion group Q = {±1,±i,±j,±k} where i² = j² = k² = −1
and ij = k, jk = i, and ki = j, are:

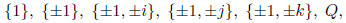
and every subgroup is normal.

4.9b Claim: Let : G → G' and : G' → G'' be homomorphisms of groups. Then

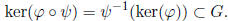
Proof. Obvious.