Elementary Number Theory
Save your current worksheet as number2.mws. Remember to save frequently in
case of system shut
downs in the middle of a work session! In the text mode (click on the cap T
button) place your name(s)
and date at the top of your worksheet. At the end of this session you will print
out and turn in your
worksheet.
We continue by experimenting with some more very basic calculations . Again
the intent is to learn some
basic MAPLE syntax, while observing more neat features of a Computer Algebra
System (CAS). We
will also review some basic concepts from number theory .
Preform the following calculations with MAPLE. You must
reenter the calculation mode (click on the [ >
button). As you do these exercises enter notes and comments onto your worksheet
in text mode.
[ > gcd( 6, 8 )
1. What is gcd an abreviation for?
[ > lcm( 6, 8 )
2. What is lcm an abreviation for?
[ > gcd( 6, 8 ) lcm( 6, 8)
[ > gcd( 140, 958 )
[ > lcm( 140, 958 )
[ > %*%%;
[ > 140*958;
3. What general formula is suggested by these calculations? Test the formula
with several more pairs
of integers.
Continue the exercises.

Notice that bigger integers don't necessarily yield bigger lcm 's.
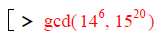
Two integers are "relatively prime" if the biggest integer that divides both
of them is 1.
4. List all the pairs of integers from 100 to 110 that are relatively prime.
Here you might want to ask
for the MAPLE Programming Supplement to learn how to do "for" and "if" programs.
An integer is called "prime" if its only divisors are 1 and itself .
The MAPLE command "isprime" determines whether or not a given integer is
prime. Use it to see if
the following numbers are prime : 29, 35, 1537, your ss#, 10!+1, 329891.
5. List the prime numbers between 1 and 100.
The FUNDAMENTAL THEOREM OF ARITHEMATIC states that every integer can be
factored in
a unique way into a product of powers of primes.
6. Use paper and pencil to factor the following into their prime decompositions:
10! , 340704. Include
your answers.
The MAPLE command "ifactor" does this automatically.
7. Use it to verify your results from above. Now factor the following numbers:
10!+1 , your ss#.
Execute the following command sequence:
[ > 2744280=ifactor(2744280);
267300=ifactor(267300);
[ > 2744280*267300=ifactor(2744280*267300);
[ > gcd(2744280,267300)=ifactor(gcd(2744280,267300));
[ > lcm(2744280,267300)=ifactor(lcm(2744280,267300));
[ > lcm(2744280,267300)*gcd(2744280,267300)=ifactor(lcm(2744280,267300
)*gcd(2744280,267300));
8. Using the FUNDAMENTAL THEOREM OF ARITHEMATIC, provide a written argument
to verify
the formula : gcd(m,n)lcm(m,n) = mn. Demonstrate your argument with two
sufficiently interesting
integers ( different from above ) and the ifactor command in MAPLE.
For two integers m & n with n > or = m we say the "remainder of n divided by
m" is r if
n = qm + r, for integers q >0 & r with 0 < or = r < m.
9. With paper and pencil compute the following remainders and include your
answers: 24 divided by 5,
156 divided by 7, 32 divided by 2, 57 divided by 4.
In MAPLE this remainder is denoted by "n mod m." Verify the above answers
with MAPLE and
compute the following remainders:
[ > 13200 mod 134
[ > ( 123 + 53 ) mod 26
[ > 400*23 mod 19;
[ > 1321 mod (5*7);
[ > 4516 mod 4
10. Explain why an integer n is "even" exactly when n mod
2 = 0, and is "odd" exactly when
n mod 2 = 1.
11. Explain why every product of two odd integers must be
an odd integer and every product of an even
integer with another integer must be even.
Do the following calculations in your head and record the answers. Check the
results with MAPLE.

| Prev | Next |